Lag prismer
Aktivitet
La oss si at du kan bruke bare to forskjellige lengder: 2 enheter og 4 enheter.
Om du bruker disse lengdene til å lage sidekantene i rektangler, hvor mange forskjellige kan du lage? Husk at kvadrat er bare en spesiell type rektangel.
Vi kan lage tre forskjellige rektangler. To av figurene ovenfor er like, bare rotert, så dem teller vi bare én gang.
Vi skal ikke lage todimensjonale rektangler, vi skal lage tredimensjonale prismer!
Ved å bruke bare disse to lengdene som sidekanter i prismer, hvor mange forskjellige kan du lage?
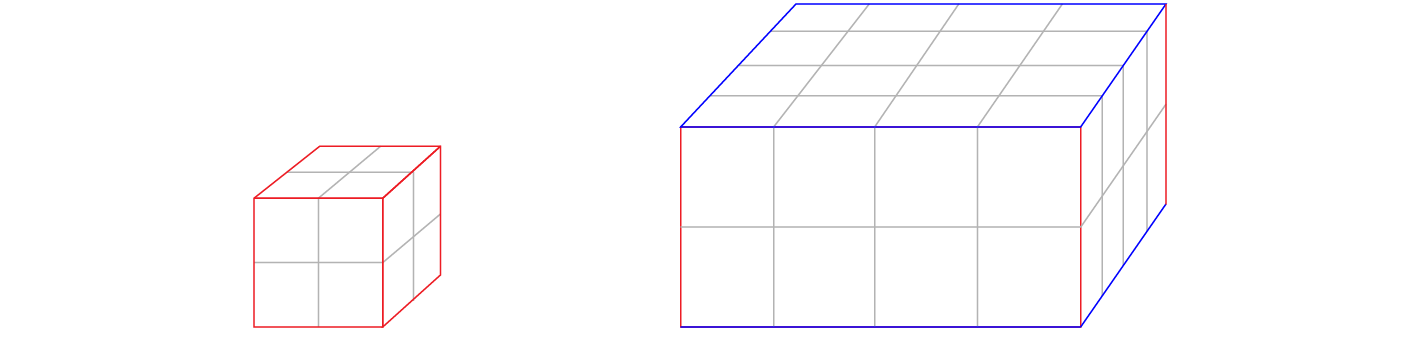
Her ser du to av prismene som kan lages. Hvor mange flere er det?
Lag prismene av centikuberEn centikube er en enhetskube, for eksempel en terning, der alle sidene er 1 cm lang. . Du må finne en god måte å holde oversikt over resultatene dine på.
Ved å lage en liste kan du holde oversikt over de to prismene på bildet ovenfor:
Den minste er \(2\cdot2\cdot2\)
Den største er \(2\cdot4\cdot4\)
Du bør finne en måte å holde oversikt på som gir mening for deg.
Hvordan kan du vite at prismene ikke er like, selv om de roteres?
Hvor mange forskjellige prismer fant du?
Hva skjer om du har tre lengder: 2 enheter, 3 enheter og 4 enheter?
Hvor mange forskjellige prismer kan du lage nå?
Husk at du må holde oversikt over resultatene dine.
Når du har laget alle prismene, kan du prøve å organisere dem etter størrelse, men hvordan skal du finne ut av det?
Starthjelp
- Hvordan kan du vite at alle prismene er forskjellige?
- Hva kan du lage ved å bruke bare lengder på 2 enheter?
- Hva kan du lage ved å bruke bare lengder på 3 enheter?
- Hva kan du lage ved å bruke bare lengder på 4 enheter?
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven fokuserer på lengden på sidekantene i prismer, i stedet for overflate eller volum av prismer. Den kan hjelpe elevene til å få bedre forståelse av strukturen i tredimensjonale figurer. Den egner seg også som en oppgave som de kan arbeide med før volum introduseres.
Mulig tilnærming
Du kan introdusere oppgaven ved å stille spørsmål til todimensjonale figurer, slik som vist på bildet i oppgaven.
Når dere har diskutert oppgaven og hva som må gjøres, kan elevene arbeide sammen i par, slik at de kan snakke med noen andre om ideene sine. Del ut centikuber.
Når den tredje lengden introduseres, bør du påpeke at arbeidet som allerede er gjort, ikke er bortkastet. Prismene som allerede er laget, er bare en del av en større familie som nå vokser. Noen elever legger nok merke til det på egen hånd.
Å lage en liste eller en tabell er en viktig og nyttig måte til å sjekke at alle muligheter er tatt med. Det kan også gjøres i fellesskap på slutten av økta. Diskuter med elevene hvordan de kan gjøre dette metodisk, slik at ingen prismer blir tatt med flere ganger, slik som \(3\cdot4\cdot2\) og \(2\cdot4\cdot3\). En måte å gjøre det på er å lage lista etter stigende tall, slik at eksemplet ovenfor alltid blir skrevet som \(2\cdot3\cdot4\)
Senere kan elevene lage fine modeller av prismene som de kan bruke i en utstilling.
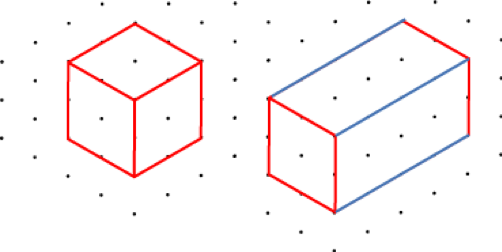
Prismene kan også tegnes på isometrisk papir.
Gode veiledningsspørsmål
- Hvilket prisme kan det være lurt å starte med?
- Hvor på prismet finner du like store sideflater?
Mulig utvidelse
Elevene kan undersøke hvor mange prismer det er mulig å lage når det legges til en lengde. Kan de forutsi hva som skjer med fem forskjellige lengder?
1 lengde – 1 prisme
2 lengder – 4 prismer
3 lengder – … prismer
4 lengder – … prismer
Ressursen er utviklet av NRICH