LAST NED kopioriginaler

Ti skjulte kvadrater

Stikkord: Kvadrat Koordinater Visualisering Systematisk arbeid

Aktivitet

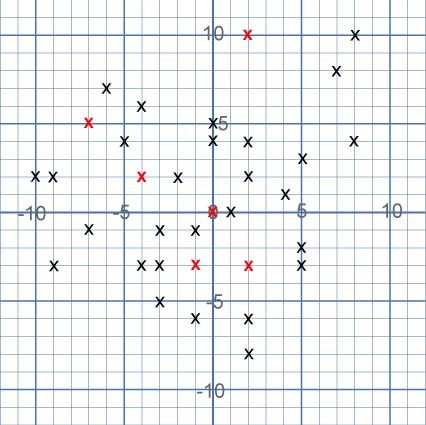
I koordinatsystemet nedenfor er det markert 34 punkter.

Koordinatsystem med 34 punkter

Alle punktene er hjørner i til sammen ti skjulte kvadrater. Hvert av de seks røde punktene deles av to kvadrater. De andre 28 punktene er hjørner i bare ett kvadrat hver. Alle kvadratene har sidekanter som skjærer minst ett annet kvadrat.

Alle kvadratene er i forskjellig størrelse. Ingen sidekanter går gjennom noen av punktene (selv om noen er nære på).

Kan du finne de ti skjulte kvadratene?

Starthjelp

  • Begynn med å se på et punkt, og let etter tre andre som danner et kvadrat sammen med det.
  • Husk at linjene i kvadratet ikke trenger å være parallelle med linjene i koordinatsystemet.

Løsning

  1. (2,-3) (-1,-3) (-1,-6) (2,-6)
  2. (0,0) (5,-3) (2,-8) (-3,-5)
  3. (0,0) (2,2) (0,4) (-2,2)
  4. (1,0) (4,1) (5,-2) (2,-3)
  5. (2,10) (8,10) (8,4) (2,4)
  6. (2,10) (7,8) (5,3) (0,5)
  7. (-1,-1) (-1,-3) (-3,-3) (-3,-1)
  8. (-4,2) (-9,2) (-9,-3) (-4,-3)
  9. (-7,5) (-10,2) (-7,-1) (-4,2)
  10. (-7,5) (-5,4) (-4,6) (-6,7)

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

Det er to aspekter ved denne oppgaven som kan være krevende for elevene. De må ha kunnskap om koordinater i alle fire kvadranter, og være trygge på egenskapene til kvadrater. Elevene får også se at et kvadrat kan orienteres, og oppgaven kan dermed også bidra til å rokke ved oppfatninger om hvordan andre figurer kan orienteres.

Mulig tilnærming

Begynn med å tegne noen figurer i et koordinatsystem ut fra koordinatene til hjørnene, med koordinater i alle fire kvadranter. Bruk denne kopioriginalen på en interaktiv tavle, eller skriv den ut i A3 og tegn direkte på den. For å hjelpe til med selve oppgaven kan det være lurt å velge noen figurer som ikke er prototypeeksempler.

Fortsett ved å velge et punkt i koordinatsystemet fra oppgaven, etterfulgt av et nytt punkt for å danne to hjørner i et kvadrat. Spør elevene hvor et tredje hjørne kan plasseres, og hvis det ikke er et kryss der, ber du om alternativer. Når det tredje hjørnet er funnet, spør du hvor det fjerde hjørnet må være for at figuren skal bli et kvadrat.

Etter introduksjonen kan elevene arbeide sammen i par med resten av oppgaven, slik at de kan diskutere tankene sine med hverandre. De kan bruke denne kopioriginalen både til kladd og til ferdigstilling. På slutten av økta bør dere oppsummere løsningsforslag i plenum.

Gode veiledningsspørsmål

  • Hvordan er kvadratet orientert i rutenettet/koordinatsystemet?
  • Hvor kan de andre hjørnene være?
  • Kan du finne et annet hjørne til dette kvadratet?

Mulig utvidelse

Elever som løser oppgaven fort, kan prøve å tegne inn flere kvadrater i dette koordinatsystemet. Sørg for at alle fortsatt er i forskjellig størrelse.

Mulig støtte

Elever som får det vanskelig, kan prøve denne oppgaven «Åtte skjulte kvadrater», som bruker koordinater bare i første kvadrant.

Ressursen er utviklet av NRICH

8,9