Teltstenger

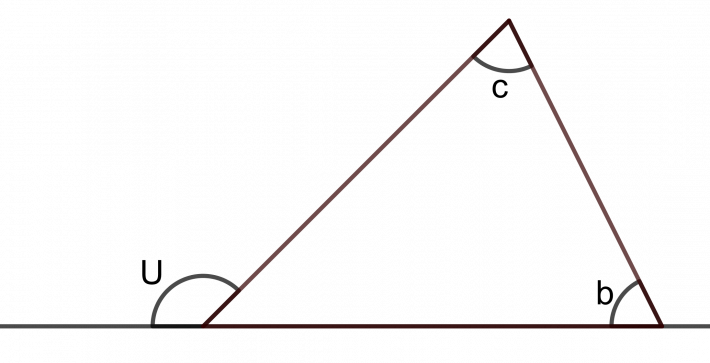
Her kan vi med fordel bruke Euklids teorem om utvendige vinkler, som sier at en utvendig vinkel i en trekant er lik summen av de to ikke-tilstøtende innvendige vinklene i trekanten.

På figuren er vinkel U = b + c (ser du hvorfor?).

Siden \(QS = SR\), er trekanten \(SQR \) likebeint, slik at \(\angle SRQ=\angle SQR=x^\circ\)

Når vi kjenner \(\angle SRQ\) og \(\angle SQR\), og tar Euklids teorem om utvendige vinkler i trekanter i betraktning, ser vi at \(\angle QST=2x^\circ\).

Siden \(QT=TS\), vet vi at også \(\angle TQS=2x^\circ\).

Siden \(PT=QT,\:\angle TPQ=\angle TQP=20^\circ\).

Vinklene i trekant \(PQR\) må være \(180^\circ\). Dermed kan vi finne verdien av \(x\) slik:

\(20+(20+2x+x)+x=180\\40+4x=180\\4x=140\\x=35\)