Skakke kvadrater
Aktivitet
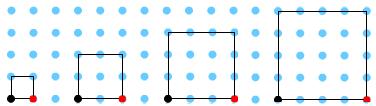
Det er enkelt å finne arealet av kvadrater som er tegnet på et rutenett, hvis de er orientert langs x-aksen og y-aksen:
Kan du finne en rask og enkel måte for å finne arealet av kvadrater som har en helling?
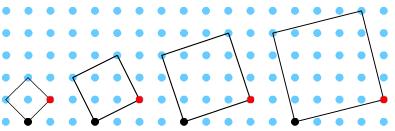
Her er noen kvadrater med en helling på 1:
Om du trenger det, kan du se på Starthjelp for å få tips til hvordan du kan beregne arealet av disse kvadratene.
Legger du merke til noe spesielt med arealene?
Kan du forutse arealet av andre kvadrater med helling på 1?
Hva med kvadrater med helling på 2, 3, 4 eller …?
Legger du merke til noe spesielt?
Kan du lage noen hypoteserEn hypotese er en gjetning, antagelse eller forklaring som synes rimelig ut fra foreliggende kunnskap, og som man forsøker å avkrefte eller bekrefte. Noen ganger betyr hypotese bare en midlertidig og hittil ubekreftet forklaring av kjente og iakttatte, men ellers uforklarte fenomener. om arealet av skakke kvadrater?
Kan du bevise hypotesene dine?
Du kan bruke GeoGebra-appleten nedenfor til å lage kvadrater.
Starthjelp
To metoder for å finne arealet av figurer kan være til hjelp.
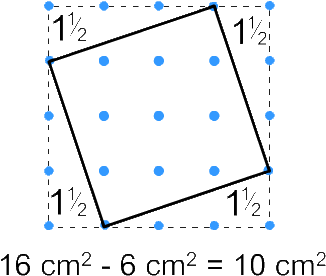
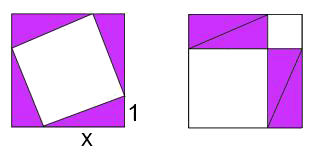
Vi kan enkelt finne arealet av et kvadrat rundt kvadratet, som på bildet nedenfor. Vi kan finne arealet av de rettvinklede trekantene, subtrahere dem fra det store kvadratet, og stå igjen med arealet av det skakke kvadratet.
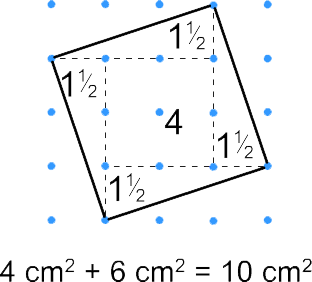
Vi kan også dele det skakke kvadratet opp i et mindre kvadrat og rettvinklede trekanter, og regne ut arealet av hver figur.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven legger til rette for mønstergjenkjenning, generalisering og eventuelt Pytagoras’ læresetning, samtidig som elevene får øving i å regne ut areal av kvadrater og rettvinklede trekanter.
Mulig tilnærming
De to kopioriginalene kan være nyttige.
Det kan være hensiktsmessig å repetere hvordan vi regner ut arealet av et kvadrat som står orientert langs x-aksen og y-aksen, før du begynner med skakke kvadrater. Du kan bruke GeoGebra-appleten til å lage noen kvadrater, og be elevene om å diskutere sammen i par hvordan de vil regne ut arealet, før noen får dele svaret sitt med resten av klassen.
«Men hva om vi skal finne arealet til et skakt kvadrat eller et kvadrat som står på skrå i rutenettet?»
Det er viktig å presisere for elevene at vi kan kalle kvadratet skakt eller skråstilt i denne oppgaven, fordi det står på skrå i forhold til x-aksen og y-aksen i rutenettet av punkter som skal brukes som hjørner i kvadratene, men at vi vanligvis ikke kaller kvadrater skråstilte, skakke eller lignende.
Bruk GeoGebra-appleten, en interaktiv tavle eller lignende, og tegn et skråstilt kvadrat, for eksempel slik:
«Hvordan kan vi finne arealet av dette kvadratet?»
Noen elever vil kanskje påstå at sidekantene er 3 cm (de kan tenke at vi beholder sidelengden i kvadratet, selv om vi stiller det på skrå som på figuren), og at arealet derfor må bli 9 kvadratcentimeter.
Andre vil kanskje foreslå å måle en sidekant med linjal og kvadrere denne lengden.
Diskuter problemene med slike påstander før du skisserer et \(4\cdot4\)-kvadrat rundt det skråstilte kvadratet, og spør elevene hvordan vi kan regne ut arealet av det skråstilte kvadratet ved hjelp av det store kvadratet. Du kan gjerne demonstrere hvordan det kan gjøres, ved å regne ut arealet av det store kvadratet og subtrahere de fire rettvinklede trekantene.
Be deretter
- en gruppe om å tegne et kvadrat med grunnlinje 4 bortover og 1 oppover.
- en gruppe om å tegne et kvadrat med grunnlinje 5 bortover og 1 oppover.
- en gruppe om å tegne et kvadrat med grunnlinje 6 bortover og 1 oppover.
- en gruppe om å tegne et kvadrat med grunnlinje 7 bortover og 1 oppover.
Alle gruppene må også finne arealet av sitt kvadrat, slik at du kan føre opp resultatene:
4 bort og 1 opp: 17
5 bort og 1 opp: 26
6 bort og 1 opp: 37
7 bort og 1 opp: 50
«Hva legger dere merke til med disse arealene?»
«Om vi hadde tegnet et kvadrat med sidelengde 8 bort og 1 opp, hva tror dere arealet ville blitt?» (65)
«Om vi hadde tegnet et kvadrat med sidelengde x bort og 1 opp, hva tror dere arealet ville blitt?» (\(x^2 +1\))
«Men hva om vi hadde tegnet et kvadrat med mer helling, for eksempel 3 bort og 2 opp, eller 4 bort og 2 opp, eller…?»
Noen vil kanskje foreslå \(x^2 +2\).
Be deretter klassen i grupper finne arealet av noen nye kvadrater med helling, og før opp resultatene:
3 bort og 1 opp: 13
4 bort og 1 opp: 20
5 bort og 1 opp: 29
6 bort og 1 opp: 40
«Stemmer hypotesen om \(x^2 +2\) (dersom den dukket opp)?»
Elevene vil kanskje se at resultatene er på formen \(x^2 +4\), eller \(x^2 +2^2\). Noen vil kanskje også konkludere med at det første eksemplet burde skrives på formen \(x^2 +1^2\).
På dette tidspunktet kan det være hensiktsmessig å bevise hypotesene om at arealene kan skrives som henholdsvis \(x^2 +1^2\) og \(x^2 +2^2\).
Du kan bruke en algebraisk tilnærming, eller spørre elevene hvorfor disse figurene beviser hypotesene:
«Hva tror dere vil skje om kvadratene har enda mer helling? For eksempel 3, 4 eller 5 oppover?»
Be elevene om å sjekke disse kvadratene i grupper også, for å se om hypotesene stemmer.
Til slutt kan en algebraisk eller visuell tilnærming til hypotesene tilpasses for å bevise Pytagoras’ setning.
Et kvadrat med x bortover og 1 oppover kan settes i et kvadrat med sidelengde x + 1.
Arealet av det skakke kvadratet er \((x+1)^2\) minus arealet av de fire rettvinklede trekantene. Dette blir \((x^2+2x+1)-2x=x^2 +1\), som er i overensstemmelse med hypotesen.
Et kvadrat med x bortover og 2 oppover kan settes i et kvadrat med sidelengde x + 2.
Arealet av det skakke kvadratet er \((x+2)^2\) minus arealet av de fire rettvinklede trekantene. Dette blir \((x^2+4x+4)-4x=x^2 +4\), som er i overensstemmelse med hypotesen.
Et kvadrat med x bortover og y oppover kan settes i et kvadrat med sidelengde x + y.
Arealet av det skakke kvadratet er \((x+y)^2\) minus arealet av de fire rettvinklede trekantene. Dette blir
\((x^2+2xy+y^2)-2xy=x^2+y^2\), som er i overensstemmelse med hypotesen.
Oppfølgingstimer kan fokusere på å finne lengder til sidene i rettvinklede trekanter, når to sidelengder er gitt.
Gode veiledningsspørsmål
- Hvordan kan du finne arealet av et skakt kvadrat i rutenettet?
- Om du tegner et kvadrat med sidelengde x bortover og 1 oppover, hva vil du forvente at arealet blir?
- Om du tegner et kvadrat med sidelengde x bortover og 2 oppover, hva vil du forvente at arealet blir?
- Om du tegner et kvadrat med sidelengde x bortover og y oppover, hva vil du forvente at arealet blir?
Mulig utvidelse
Det er mulig å tegne kvadrater med areal 1, 2, 4, 5, 8, 9 …, men ikke med 3, 6, 7, 11, 12 …
Elevene kan utforske egenskapene til tall som er mulige, og tall som ikke er mulige som areal av skakke kvadrater i rutenettet.
Kan de bevise at tall på formen 4n + 3 ikke er mulige arealer?
Mulig støtte
Begynn med Lag kvadrater! eller Kvadrater med koordinater, for å hjelpe elevene til å bli trygge på å tegne skakke kvadrater.
Ressursen er utviklet av NRICH