Vinkler i en tolvkant
Problem
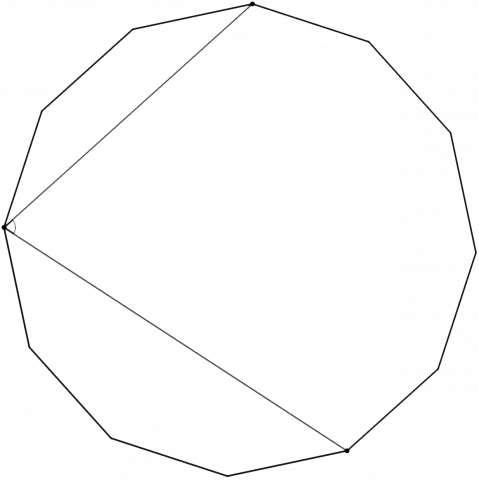
Figuren viser en regulær tolvkant (dodekagon), en mangekant med tolv like lange sider hvor alle vinklene er like store.
Hvor stor er den markerte vinkelen inne i tolvkanten?
Løsning
Hver side i tolvkanten spenner over en vinkel på \(360^\circ : 12 = 30^\circ\) i sirkelen som går gjennom alle hjørnene i tolvkanten (tolvkantens omskrevne sirkel).
Vi tenker oss vinkelen satt sammen av to deler:
\(\angle AOP = 90 ^\circ\\ \angle OPA = 45^\circ\)
og
\(\angle BOP = 120^\circ\\ \angle OPB = 30^\circ\)
Da blir
\(\angle APB = 45^\circ +30^\circ = 75^\circ\)
Alternativt:
\(\angle AOB = 5 \cdot 30^\circ = 150^\circ\)
En periferivinkel er alltid halvparten så stor som en sentralvinkel, så
\(\angle APB = 75^\circ\)
Ressursen er utviklet av NRICH
9