Kvadrater med koordinater
Aktivitet
Prøv å lage mange ulike kvadrater i koordinatsystemet i denne appleten. Figuren blir farget når den er kvadratisk.
Prøv å lage kvadrater der sidene ikke følger linjene i koordinatsystemet.
Forklar hvordan du kan lage et kvadrat når du har fått oppgitt koordinatene til to punkter som skal danne endepunktene på en sidelinje. Prøv å lage en generell regel.
Forklar hvordan du kan lage et kvadrat når du får oppgitt koordinatene til to punkter som skal danne endepunktene til en diagonal. Prøv å lage en generell regel.
Avgjør om noen av punktene nedenfor danner hjørnene i et kvadrat. I tilfelle hvilke?
Kan du avgjøre dette uten å tegne punktene inn i koordinatsystemet?
- (8, 3), (7, 8), (2, 7), (3, 2)
- (3, 3), (7, 4), (8, 8), (4, 7)
- (16, 19), (18, 22), (21, 20), (19, 17)
- (4, 20), (21, 19), (20, 2), (3, 3)
Forklar hvordan du tenkte!
Starthjelp
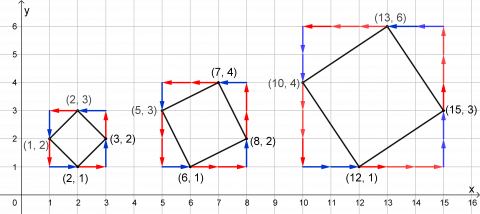
- Studer det som skjer med koordinatene når du følger pilene og går fra punkt til punkt rundt kvadratet. Kan du finne et system?
- Ser du et mønster med røde og blå piler?
Løsning
Her kan en forklare på mange måter. Forklaringene nedenfor er eksempler på hvordan en kan se på problemet.
Vi ser på den midterste figuren under Starthjelp og tenker oss at vi har fått oppgitt koordinatene (6, 1) og (8, 2). Stegene fra hjørne til hjørne kan beskrives slik:
| Kvadratets sider | x-koordinat | y-koordinat |
|---|---|---|
| Fra (6, 1) til (8, 2) | +2 | +1 |
| Fra (8, 2) til (7, 4) | -1 | +2 |
| Fra (7, 4) til (5, 3) | -2 | -1 |
| Fra (5, 3) til (6, 1) | +1 | -2 |
Trinnene med lengde 2 og 1 går vekselvis i x-retning og i y-retning. Det må være slik at to påfølgende trinn i både x-koordinat og y-koordinat må ha samme retning, og dermed samme fortegn. Men de må være forskjøvet i forhold til hverandre, og det kan ikke være bare ett eller tre eller fire trinn med samme fortegn. Det kan heller ikke være to linjer etter hverandre med samme fortegn for både x-koordinaten og y-koordinaten.
1. (8, 3), (7, 8), (2,7), (3,2) danner et kvadrat.
| Kvadratets sider | x-koordinat | y-koordinat |
|---|---|---|
| Fra (8, 3) til (7, 8) | -1 | +5 |
| Fra (7, 8) til (2, 7) | -5 | +1 |
| Fra (2, 7) til (3, 2) | +1 | -5 |
| Fra (3, 2) til (8, 3) | +5 | +1 |
Her ser vi samme mønster som ovenfor.
2. (3, 3), (7, 4), (8, 8), (4, 7) er ikke et kvadrat:
| Kvadratets sider | x-koordinat | y-koordinat |
|---|---|---|
| Fra (3, 3) til (7, 4) | +4 | +1 |
| Fra (7, 4) til (8, 8) | +1 | +4 |
| Fra (8, 8) til (4, 7) | -2 | -3 |
| Fra (4, 7) til (3, 3) | -1 | -4 |
Tallene følger samme mønster som ovenfor, men ikke fortegnene. To og to linjer har samme fortegn for både x-koordinatene og y-koordinatene.
3. (16, 19), (18, 22), (21, 20), (19, 17) er et kvadrat.
| Kvadratets sider | x-koordinat | y-koordinat |
|---|---|---|
| Fra (16, 19) til (18, 22) | +2 | +3 |
| Fra (18, 22) til (21, 20) | +3 | -2 |
| Fra (21, 20) til (19, 17) | -2 | -3 |
| Fra (19, 17) til (16, 19) | -3 | +2 |
4. (4, 20), (21, 19), (20, 2), (3, 3) er et kvadrat.
| Kvadratets sider | x-koordinat | y-koordinat |
|---|---|---|
| Fra (4, 20) til (21, 19) | +17 | -1 |
| Fra (21, 19) til (20, 2) | -1 | -17 |
| Fra (20, 2) til (3, 3) | -17 | +1 |
| Fra (3, 3) til (4, 20) | +1 | +17 |
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten vil å få elevene til å se at kvadrater ikke nødvendigvis må ha den tradisjonelle orienteringen med to sider liggende horisontalt.
Oppgaven utfordrer elevene til å visualisere sammenhengen mellom koordinatene til hjørnene i et kvadrat.
Den interaktive GeoGebrafilen kan dessuten være nyttig når Pytagoras’ setning skal introduseres, og når dere skal arbeide med stigningstallene til linjer som står normalt på hverandre.
Mulig tilnærming
Vis den appleten på tavla. Oppmuntre frivillige til å komme og lage kvadrater i koordinatsystemet.
Plasser så et par hjørner fast, og be elevene fullføre kvadratet. La dem få se koordinatene til punktene.
Deretter kan du plassere to faste punkter der alle koordinatene er enten partall eller oddetall. Utfordre elevene til å fullføre et kvadrat med disse punktene som motstående hjørner.
La elevene samarbeide parvis (med én PC) med å lage kvadrater til de kan besvare alle spørsmålene nedenfor. Be dem lage mange kvadrater, både store og små, og notere koordinatene til hjørnene.
- Hvordan kan vi tegne et kvadrat når vi får oppgitt to hjørner som ligger ved siden av hverandre?
- Hvordan kan vi tegne et kvadrat når vi får oppgitt to punkter som ligger i motstående hjørner?
- Hvordan kan vi tegne et kvadrat når vi får oppgitt ett hjørnepunkt og midtpunktet i kvadratet? (Kanskje må dere snakke om hva som menes med midtpunktet i et kvadrat.)
- Hvordan kan vi avgjøre om fire gitte punkt danner et kvadrat?
- Kan vi løse alle disse problemene uten å tegne?
Dere må oppsummere i fellesskap, se på ulike løsninger, vurdere dem og sjekke at de er holdbare. Det siste spørsmålet må elevene løse uten tegneprogram.
Denne kopioriginalen inneholder tilsvarende oppgaver som kan løses på papir.
Mulig utvidelse
- Hvordan kan dette problemet utvides til rektangler?
- Hvis du får oppgitt tre koordinater, hvordan kan du avgjøre om de vil definere en rett vinkel?
- Tegn kvadrater i koordinatsystemet med så mange ulike heltallige arealer som mulig. Hvilke arealer er mulige å tegne, og hvilke er det ikke?
Mulig støtte
Gi elevene et ark med noen kvadrater som er tiltet (dvs. ikke har sider som er parallelle med koordinataksene), og be dem tegne et kvadrat med sider parallelle med koordinataksene rundt. (Se for eksempel figur 1 under Starthjelp.) La elevene finne de fire rettvinklede trekantene som dannes rundt det indre kvadratet, og forklare hvorfor de er kongruente.
Hvis noen synes det er vanskelig å se om punktene i oppgave 1–4 danner kvadrater, kan de plotte punktene inn i koordinatsystemet, tegne en firkant mellom dem, og så tegne et kvadrat med sider parallelle med koordinataksene rundt.
Ressursen er utviklet av NRICH