LAST NED kopioriginaler

Dragen i kvadratet

Stikkord: Areal Lengder Vinkler Argumentasjon Bevis

Aktivitet

ABCD er et kvadrat. M er midtpunktet på siden AB.

Ved å tegne linjene AC, MC, BD og MD får vi en firkant med drageform. Den er farget blå.

Hvor stor del av kvadratet er farget?

Kvadrat delt opp slik at det skal ligne en drage
Figur 1

Nedenfor finner du tre ulike metoder for å finne det fargede arealet. Dessverre har punktene i resonnementene blitt blandet. Kan du sette dem i riktig rekkefølge?

Formlike figurer

Vis/skjul

Kvadrat delt opp slik at det skal ligne en drage
Figur 2
  1. Linja AC skjærer linja MD i punktet E. Vinklene MEF og AED er toppvinkler og dermed like store.
  2. Linja MF er halvparten av linja AD.
  3. Linjene AD og MF er parallelle, så vinklene EDA og EMF er like store, og vinklene EAD og EFM er like store fordi de er samsvarende vinkler ved paralleller.
  4. Derfor er trekantene AED og FEM formlike.
  5. Derfor er linja EH halvparten så lang som PE.
  6. La ABCD være et enhetskvadrat (dvs. at det har sidelengde 1 lengdeenhet og areal 1 arealenhet).
  7. Derfor er det fargede arealet MEFG = \(\frac{1}{24}\cdot2=\frac{1}{12}\) arealenheter.
  8. PH har lengde \(\frac{1}{2}\) lengdeenhet, så PE har lengde \(\frac{1}{3} \) enhet og EH har lengde \(\frac{1}{6}\) enhet.
  9. Trekanten MEF har areal \(\frac{1}{2}\ \cdot\left(\frac{1}{2}\ \cdot\ \frac{1}{6}\right)=\ \frac{1}{24}\) arealenheter.

Punktene A–I ovenfor kan skrives ut fra kopioriginalen. Du kan klippe det opp slik at det er lettere å legge punktene i riktig rekkefølge.

Pytogoras’ setning

Vis/skjul

Kvadrat delt opp slik at det skal ligne en drage
Figur 3
  1. Arealet av ΔDMC = 2 arealenheter.
    a) Arealet av ΔDFC = 1 arealenhet.           
    b) Dermed er arealet av ΔDFE, ΔCFG og det fargede arealet MEFG til sammen 1 arealenhet.
  2. ​​​​​​
    ​\(EH^2+HF^2=EF^2\\\quad\\ {\rm{a)}}\:EH=HF\\ \\ {\rm{b)}} \:EH^2=\frac{EF^2}{2}\\\\ {\rm{c)}}\:EH=\frac{EF}{\sqrt2}\)      ​​

`EH^(2) + HF^(2)= EF^(2)`

a) `EH = HF`

b) `EH^(2) = (1)/(2)EF^(2)`

c) `EH = (EF)/(sqrt(2))`

 

  1. Arealene av ΔDFE, ΔCFG og det fargelagte arealet MEFG er like store, så hver av dem må ha et areal på \(\frac{1}{3}\) arealenheter.
  2. Arealet av ΔMEF = \(\frac12(1\cdot EH)=\frac12\cdot \frac{EF}{\sqrt2}\).
  3. Vi bruker Pytagoras’ setning og finner at DF har lengde √2.
  4. Totalt areal av hele kvadratet er 4 arealenheter, så det fargede arealet er \(\frac{1}{12}\) av kvadratets areal.
  5. Arealet av ΔDFE = \(\frac{DF\cdot EF}{2}=\frac{\sqrt2 \cdot EF}{2}=\frac{EF}{\sqrt2}\).
  6. Det fargelagte arealet MEFG er altså lik arealet av ΔDFE.
  7. Anta at sidene i kvadratet er 2 lengdeenheter. Da er både DJ og FJ 1 lengdeenhet.

Punktene A–I ovenfor kan skrives ut fra kopioriginalen. Du kan klippe det opp slik at det er lettere å legge punktene i riktig rekkefølge.

Koordinater

Vis/skjul

Kvadrat delt opp slik at det skal ligne en drage
Figur 4
  1. Det fargede arealet består av to kongruente trekanter. Koordinatene til hjørnene i den ene av trekantene er \((\frac13, \frac 23),(\frac12, \frac 12), (\frac 12,1)\).
  2. Linja mellom (0, 0) og \((\frac 12,1)\) har likningen y = 2x.
  3. Arealet av trekanten er \(\frac12 (\frac12 \cdot \frac16)=\frac{1}{24}\).
  4. Linja mellom (0, 1) og (1, 0) har likningen y = 1 – x.
  5. Derfor er det fargede arealet \(2 \cdot \frac{1}{24}=\frac {1}{12}\).
  6. Punktet (a, b) er skjæringspunktet mellom linjene y = 2x og y = 1 – x.
  7. Vi tenker oss et enhetskvadrat tegnet inn i koordinatsystemet.
  8. Trekantens høyde er \(\frac12 - \frac13= \frac16\).
  9. Så \(a=\frac13, b=\frac23\).
  10. Linja mellom (0, 0) og (1, 1) har likningen y = x.

Punktene A–J ovenfor kan skrives ut fra kopioriginalen. Du kan klippe det opp slik at det er lettere å legge punktene i riktig rekkefølge.

 

Starthjelp

For metoden med formlike trekanter:

  • Hvilke vinkler er like store?
  • Hvilke lengder kjenner vi?

For metoden med Pytagoras’ setning:

  • Hvor finnes det rette vinkler i figuren?
  • Hvilke lengder kjenner vi?

For metoden med koordinater:

  • Hva er likningene til linjene i figuren?
  • Hvor skjærer de hverandre?
     

Løsning

Riktig rekkefølge av punktene er slik:

For metoden med formlike trekanter:

F, C, A, D, B, E, H, I, G

For metoden med Pytagoras’ setning:

I, E, G, B, D, H, A, C, F

For metoden med koordinater:

G, J, B, D, F, I, A, H, C, E

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

Mange elever synes geometriske bevis er vanskelige. I denne oppgaven er tre ulike bevis presentert, men rekkefølgen av de ulike utsagnene i bevisene er blandet. Det gir elevene anledning til å arbeide med geometriske bevis uten å måtte lage dem selv.

Mulig tilnærming

Oppgaven kan skrives ut her.

Du finner også kopioriginaler der elevene kan klippe ut alle utsagnene i de tre bevisene. Det kan gjøre det lettere å sette dem i riktig rekkefølge: Formlike trekanter, Pytagoras’ setning og Koordinater.

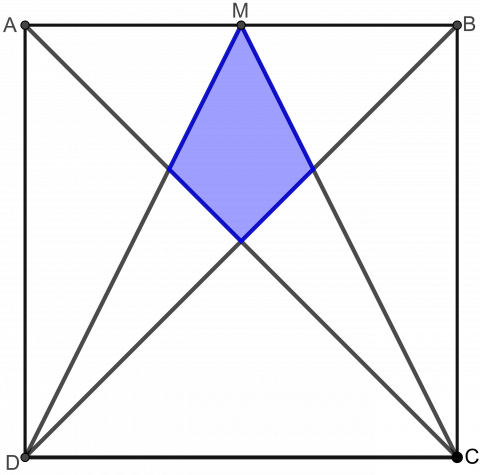
Vis elevene figuren i oppgaven.

«ABCD er et kvadrat. M er midtpunktet på AB. Hvor stor del av figuren er farget?»

Gi elevene tid til å prøve å løse problemet. Mens de arbeider, kan du gå rundt og merke deg hvilke metoder de prøver å bruke.

Etter en stund kan hele klassen samles. Løsningen på denne oppgaven er ikke så åpenbar, det kan være godt å se at mange har vanskeligheter med å løse den. 

«Jeg har fått løsninger fra tre personer som har løst problemet på ulike måter. Dessverre har løsningene blitt rotet til, så det de har skrevet, er kommet i feil rekkefølge. Kan dere sette utsagnene i riktig rekkefølge, slik at det blir et logisk argument?»

Del ut konvolutter med hver metode, la elevene arbeide to eller tre sammen. De kan klippe opp arkene slik at de kan flytte utsagnene rundt. (Eventuelt kan du ha klipt opp alt på forhånd. Men da må elevene i tillegg få figuren som følger til de ulike løsningene, for det henvises til ulike navn på punkter osv.) Det kan være lurt å trykke de ulike metodene på ark med ulike farger, slik at de ikke blir blandet sammen.

«Prøv å samarbeide om å sette utsagnene i hvert bevis i riktig rekkefølge. Når dere har funnet en løsning, kan en i gruppa gjengi resonnementet til de andre uten å se på kortene!»

Hvis metoden med koordinater skulle være ukjent for elevene, kan dere bruke bare de to andre metodene.

Så snart elevene har arbeidet grundig med bevisene, satt dem sammen og reprodusert dem for hverandre uten å se på arkene, er det tid for å avrunde i samlet klasse. Inviter elevene til å presentere løsningene sine for klassen, og diskuter til slutt fordeler og ulemper med hver av metodene.

Gode veiledningsspørsmål

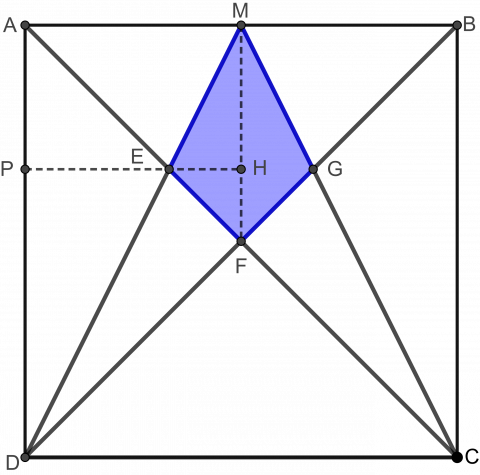
For metoden med formlike trekanter:

  • Hvilke vinkler er like store?
  • Hvilke lengder kjenner vi?

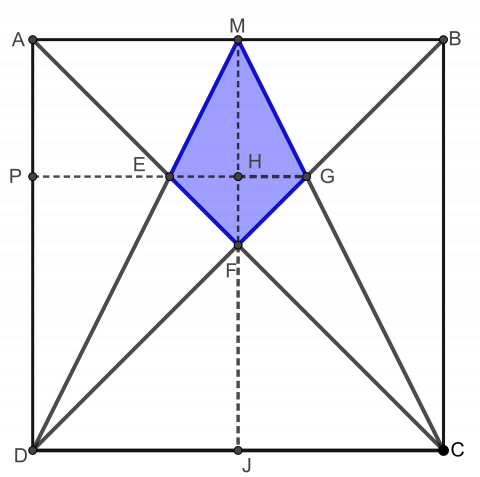
For metoden med Pytagoras’ setning:

  • Hvor finnes det rette vinkler i figuren?
  • Hvilke lengder kjenner vi?

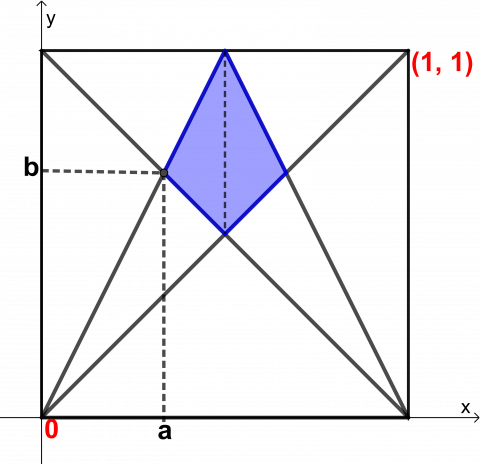
For metoden med koordinater:

  • Hva er likningene til linjene i figuren?
  • Hvor skjærer de hverandre?

Mulig støtte

Begynn med å tegne et kvadrat på et ruteark, 2 x 2 ruter til å begynne med. Forklar at vi kan tegne rette linjer mellom hjørner og midtpunkt på sidene.

Utfordre elevene til å fargelegge ulike deler, trekanter og firkanter, inne i figuren, og prøve å finne ut hvor stor del av kvadratet de har fargelagt.

Ressursen er utviklet av NRICH

9,10