Trippel Pytagoras
Problem
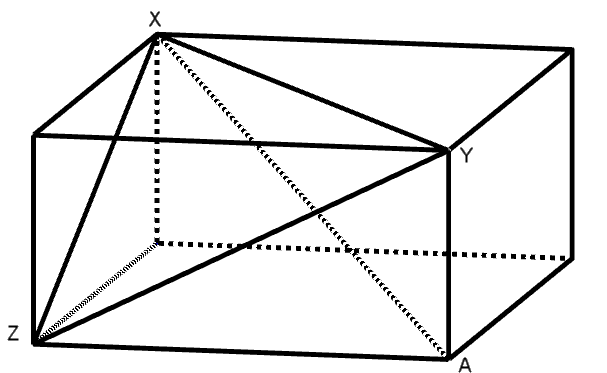
Figuren viser et rett, firkantet prisme.
I trekanten XYZ er lengdene XY, XZ og YZ henholdsvis 9, 8 og \(\sqrt55.\)
Hvor lang er diagonalen XA?
Løsning
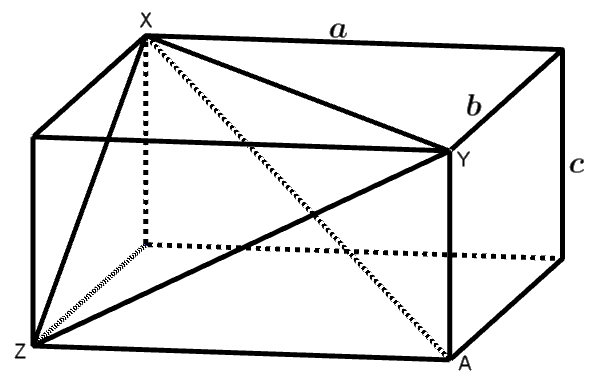
Vi kaller sidelengdene i prismet a, b og c, slik figuren viser.
Lengden XA er hypotenusen i den blå rettvinklede trekanten med sider c og k, der \(\angle ABX= 90^\circ.\text{Så }(XA)^2=c^2+k^2\).
Og k er hypotenus i en rettvinklet trekant med kateter a og b, der \(\angle AZB= 90^\circ\). Så \(k^2=a^2+b^2\).
Vi setter inn \( k^2=a^2+b^2\) i uttrykket for \((XA)^2\) og får \((XA)^2=a^2+b^2+c^2\).
\(XY = 9, \text{så } XY = AB = 9, \text{ og } (AB)^2= a^2+b^2=9^2=81\).
\(\angle XCZ=90^\circ \text{ og } XZ = 8, \text{ så } b^2+c^2= 8^2=64.\)
\(\angle YAZ=90^\circ \text{ og } YZ = \sqrt{55},\text{ så } a^2+c^2=\sqrt{55}^2=55\).
Oppsummert har vi:
\(\begin{align}a^2+b^2+b^2+c^2+a^2+c^2&=81+64+55\\ 2(a^2+b^2+c^2)&=200\\ a^2+b^2+c^2&=100\\ (XA)^2&=100\\ XA&=10\\ \end{align}\)
Ressursen er utviklet av NRICH