Trigonometrisk likhet
Problem
Figuren viser en enhetssirkelenEnhetssirkelen er en sirkel der radien er 1 og omkretsen er 2π. Det er vanlig å sette sirkelen i et koordinatsystem, med sentrum i origo. med sentrum i O.
Bruk figuren til å utlede en formel for \(\sin 2u \)
Løsning
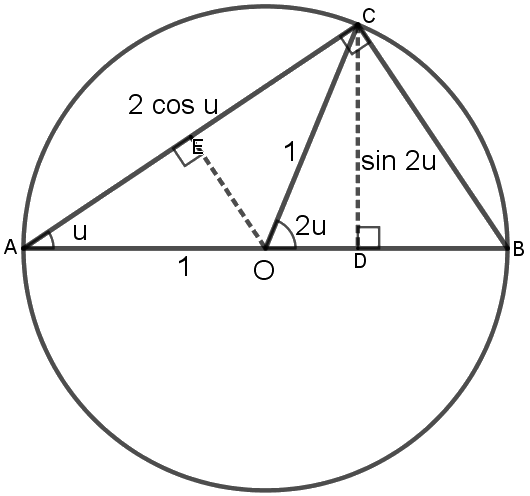
Sentralvinkelen BOC spenner over samme bue som periferivinkelen BAC. Da er vinkel BOC = 2u.
Vi har mange rettvinklede trekanter:
\(\bigtriangleup AOE \text{ gir } AE = \cos u, \text{ så } AC = 2\cos u.\\ \bigtriangleup ODC \text{ gir } CD = \sin 2u. \)
\(\text{I}\bigtriangleup ADC \text{ er } \sin u = \frac{\sin 2u}{2\cos u}\), og denne likningen gir oss sammenhengen
\(\sin 2u = 2 \sin u \cos u\)
Ressursen er utviklet av NRICH
10