Tangens i en iskrem
Problem
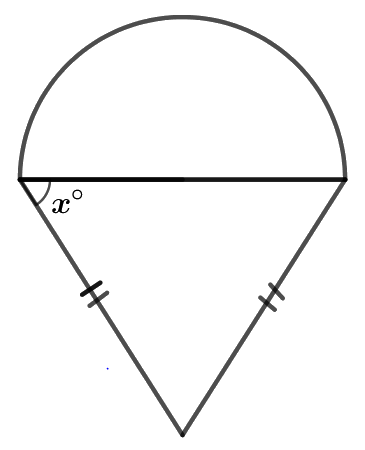
Figuren viser en halvsirkel og en likebeint trekant som har like store areal.
Finn \(\tan x^\circ\).
Løsning
La radien i halvsirkelen være \(r\) og høyden i trekanten \(h\).
\(\tan x^\circ=\frac{h}{r}\)
Arealet av halvsirkelen er \(\frac12 \pi r^2\)
Arealet av trekanten er \(\frac 12 \cdot2rh=rh\)
Disse arealene skal være like store:
\(\frac12 \pi r^2=rh\\ \frac12\pi r=h\\ \tan x^\circ=\frac{h}{r}=\frac{\pi}{2}\)
Ressursen er utviklet av NRICH
10