Så mange sirkler!
Problem
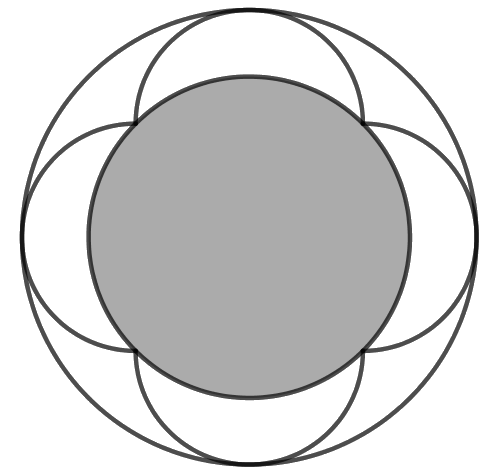
Figuren viser to sirkler og fire like store halvsirkelbuer. Arealet av den indre grå sirkelen er 1.
Hvor stort er arealet av den ytre sirkelen?
Starthjelp
- Hvor vil sentrum i de fire halvsirklene ligge?
- Tegn inn diametrene i alle halvsirklene.
Løsning
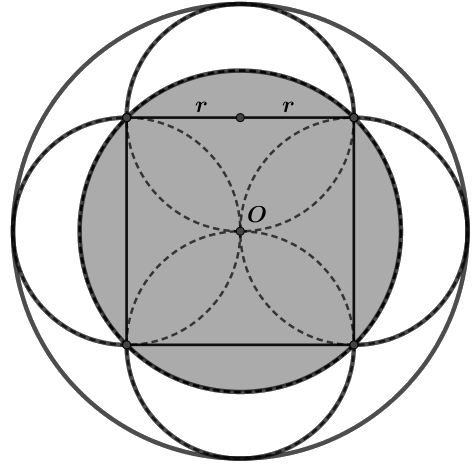
Ut fra symmetrien i figuren vet vi at de to sirklene må være konsentriske, dvs. at de har sentrum i samme punkt. Kall dette punktet O.
La radiene i de fire halvsirklene være r.
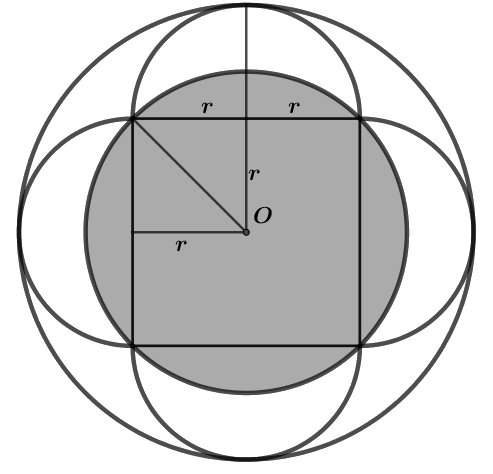
Skjæringspunktene mellom halvsirklene og den indre sirkelen vil bli hjørnene i et kvadrat med sidelengder 2r. Sentrum i halvsirklene ligger midt på hver side i kvadratet. Den ytre sirkelens radius blir 2r.
Den indre sirkelens radius blir \(\sqrt{r^2+r^2} = \sqrt2 r\)
Forholdet mellom radiene i den lille og den store sirkelen er \(\sqrt2 r:2r =\sqrt2:2=1 : \sqrt2\)
Da er forholdet mellom arealene av de to sirklene \(1^2:(\sqrt2)^2 = 1 : 2\)
Altså er arealet av den ytre sirkelen 2.
Ressursen er utviklet av NRICH