Sammenlign arealer
Aktivitet
ABC er en likebeint, rettvinklet trekant.
I hvert av de tre tilfellene nedenfor har den en innskrevet figur.
Hvilken av de tre innskrevne figurene har størst areal?
Starthjelp
• Hvilke linjestykker er like lange i figurene?
• Hvilke vinkler er like?
• La AB = BC = 12 cm. Tegn figurene.
• Hvilket av kvadratene har størst areal? Hvordan kan du vite det?
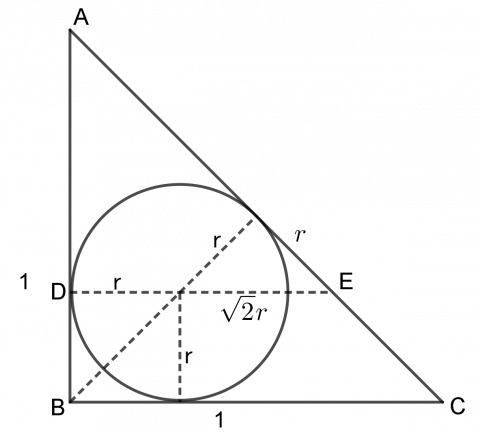
• Tegn radiene fra de tre punktene der sirkelen tangerer trekanten. Hvis radien har lengde r, kan du da finne trekantens hypotenus uttrykt ved r?
Løsning
Sirkelen har størst areal av de tre innskrevne figurene.
Utregning:
Vi setter AB = BC = 1.
Trekanten ADE er likebeint og rettvinklet, så AD = DE.
\(1-r=r+\sqrt2 r\\ (2+\sqrt2) r= 1\\ r=\frac{1(2-\sqrt2)}{(2+\sqrt2)(2-\sqrt2)}\\ r=\frac{2-\sqrt2}{2} \)
Arealet av sirkelen blir:
\(\pi r^2=\\ \pi (\frac{2-\sqrt2}{2})^2=\\ \pi \frac{6-4\sqrt2}{4}=\\ \pi \frac{3-2\sqrt2}{2}\\ \approx 0,27\)
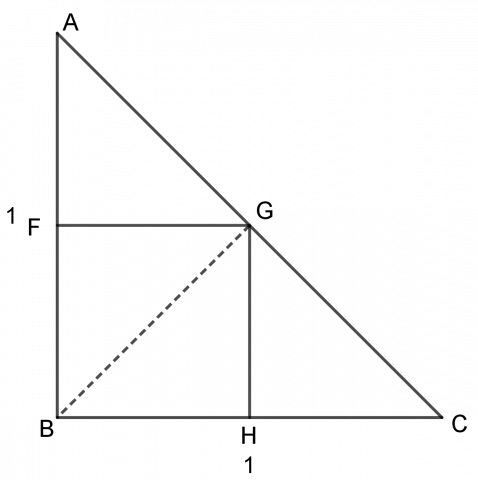
Linjestykkene FG, BG og GH deler trekanten i fire kongruente trekanter. To av dem utgjør arealet av det innskrevne kvadratet, så det har et areal som er halvparten av trekantens areal:
\(\frac12\cdot \frac {1\cdot1}{2}=\frac14 = 0,25\)
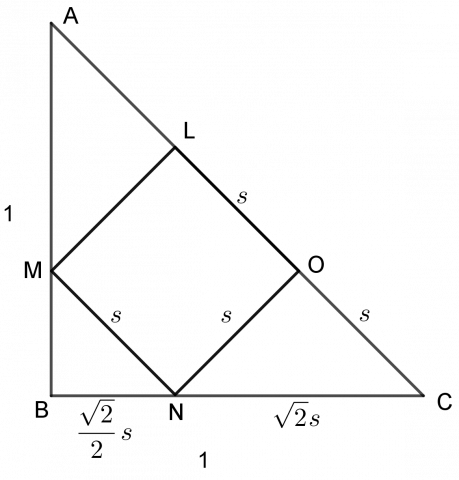
Vi kaller sidene i det innskrevne kvadratet for s. Trekantene ONC og MBN er begge rettvinklede og likebeinte, så vi kan finne BN og NC, se figuren.
Vi finner først s:
\(\frac{\sqrt2}{2} s+\sqrt2 s=1\\ \frac{3\sqrt2}{2} s = 1\\ s=\frac{2}{3\sqrt2}=\frac{\sqrt2}{3}\)
Arealet av kvadratet er
\(s^2=\frac29\approx 0,22\)
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet kobler sammen kunnskapen om sirkler og kvadrater, Pytagoras’ setning og egenskapene til tangenter til en sirkel.
Mulig tilnærming
Oppgaven kan skrives ut fra denne kopioriginalen.
Dere kan begynne med den midterste oppgaven, som er den enkleste. I de neste får dere bruk for sammenhengen mellom sidene i en rettvinklet, likebeint trekant.
Gode veiledningsspørsmål
• Hvis du kjenner lengden til katetene i en likebeint, rettvinklet trekant, hvor lang er da hypotenusen?
• Hvilke linjestykker er like lange i figurene?
• Hvilke vinkler er like store?
• Kan du bruke symmetri i figurene til hjelp?
Ressursen er utviklet av NRICH