Rette linjer – et spill for to
Aktivitet
Målet med dette spillet er å lage flest mulig rette linjer gjennom tre punkter i koordinatsystemet. Det er et spill for to, med to terninger.
Spilleregler:
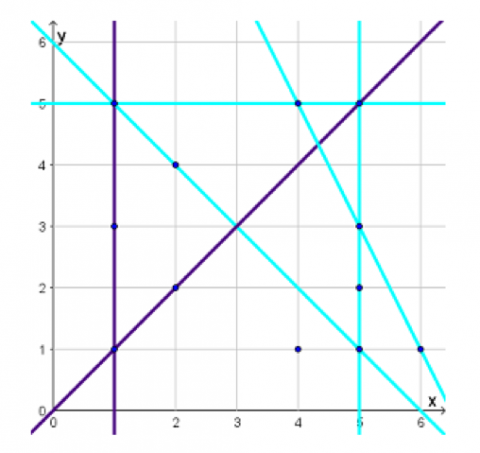
Spiller 1 kaster terningene og bruker tallene på terningene som koordinater. Hun kan fritt velge mellom mulige kombinasjoner. For eksempel gir terningkast 2 og 5 følgende mulige koordinater: \((2,5)\) og \((5,2)\). Spilleren markerer den valgte kombinasjonen i koordinatsystemet (se kopioriginal). Spiller 2 gjør deretter det samme.
Spiller 1 og spiller 2 bytter på å plassere mange punkter i koordinatsystemet. Begge spillere kan bruke alle punktene. Når en spiller oppdager at hun kan legge inn det nye punktet, slik at tre punkter ligger på en linje, tegner hun linjen med sin farge. Spilleren får da 1 poeng. Noen ganger er det mulig å lage flere linjer i ett trekk. Spilleren får da 1 poeng for hver linje. Det gjelder også hvis hun kan tegne linjer gjennom gamle punkter.
Vinneren er den som har flest poeng til slutt.
En større utfordring kan være å tillate negative tall i koordinatene. Da kan man velge fritt mellom flere mulige kombinasjoner. For eksempel gir terningkast 2 og 5 følgende mulige koordinater:\((2,5)\), \((5,2)\), \((-2,5)\), \((–2,–5)\), \((–5,2)\), \((5,–2)\) og \((–5,–2)\).
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Spillet legger til rette for at elevene kan utvikle sin forståelse av plasseringen av koordinater i koordinatsystemet.
Mulig tilnærming
Gjennomgå spillereglene muntlig. Det kan være greit å ha reglene tilgjengelig for elevene, for eksempel ved å ha spillet synlig på en Smart Board.
Mulig utvidelse
Det er mulig å utvide spillet ved å ta i bruk terninger med flere sider, for eksempel med 9 eller 12 sider. I så fall må spillerne tegne sitt eget koordinatsystem, siden kopioriginalen er tilpasset standardterninger.
Mulig støtte
Dersom elevene synes det er vanskelig å finne linjer, kan du be dem undersøke hva som skal til for at punkter ligger på samme linje. Hvis de allerede har funnet en linje, kan de ta utgangspunkt i den for å finne ut hvordan de kommer seg fra ett punkt på linjen til et annet punkt på linjen, for eksempel «en til høyre, en ned». Her har vi laget et opplegg med bare positive koordinater. Antall muligheter elevene kan velge for å avsette punkter, er dermed svært begrenset. For hvert terningkast finnes det bare to muligheter, og når de er valgt, kan elevene ikke avsette nye punkter i denne omgangen.
Ressursen er utviklet av Matematikksenteret