Hvilke lister hører sammen?
Aktivitet
Alise har arbeidet en periode med å samle værdata. Hun har en samling med gjennomsnittstemperaturer for mange dager, målt i fahrenheit.
Karl har også samlet data. Han har en lang liste med vekta til tenåringer, målt i kg.
Både Alise og Karl har samlet dataene sine i lister på 40 og 40 for å analysere dem. Uheldigvis glemte de å merke listene sine, og så husket de ikke hvilke lister som hørte til hvilke av de to samlingene.
Alise husket at liste A kom fra hennes værdata, og Karl kunne huske at liste B var vekta til 40 tenåringer. Kan du finne ut hvilke av de andre listene som hører til Alise, og hvilke som hører til Karl?
Lista nedenfor kan du også finne i et regneark her.
OBS! Hvis du vil se hvilke temperaturer det er snakk om i celsiusgrader, er omregningsformelen mellom fahrenheitskalaen og celsiusskalen slik: \(^\circ C=\frac{5(^\circ F-32)}9\)
Starthjelp
- Lag et søylediagram eller linjediagram av dataene for hver kolonne. Kan det fortelle deg noe om forskjellene på datasettene?
- Eller du kan lage boks-plot (se «Hvilket boks-plot passer?»)
- Hva er hovedtrekkene i de seks diagrammene?
- Hvilke hovedtrekk har disse diagrammene til felles?
- Er det noen hovedtrekk som kan hjelpe deg med å skille diagrammene i to grupper?
- Hvis du ser at det er to «typer» diagram, hva kan avgjøre om det dreier seg om temperaturer eller vekt?
Løsning
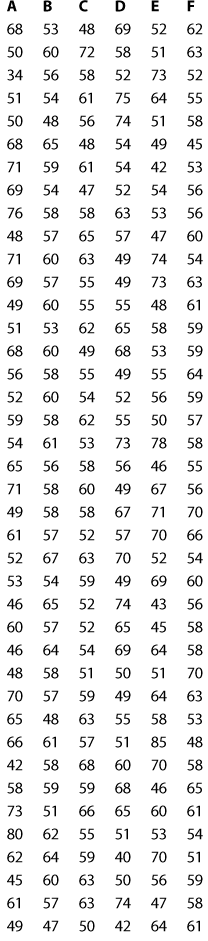
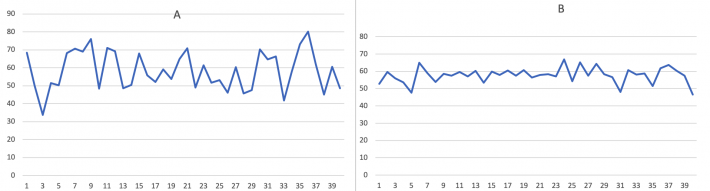
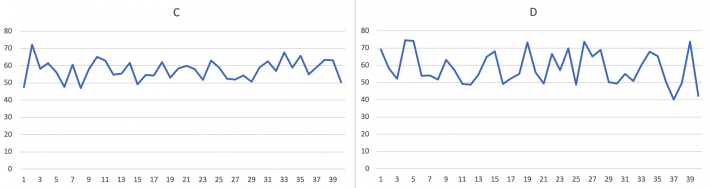
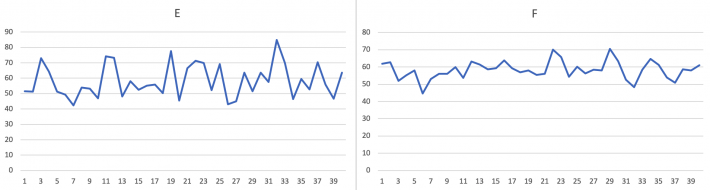
Her er det tegnet linjediagram av tallene i hver kolonne:
Du kunne også ha valgt å tegne for eksempel boks-plot eller søylediagram.
I alle linjediagrammene varierer verdiene en god del, det går mye opp og ned. Men det er større variasjon i tallene i tre av diagrammene, A, D og E, enn i de tre andre.
I regnearket kan vi også regne ut gjennomsnittsverdier og standardavvik for hver liste:
| A | B | C | D | E | F | |
| 58,4 | 57,7 | 57,6 | 58,3 | 58,3 | 58,2 | Gjennomsnitt |
| 10,826 | 4,527 | 5,756 | 10,742 | 10,742 | 5,229 | Standardavvik |
Alle listene har omtrent like stor gjennomsnittsverdi. Det er ikke et hovedtrekk som kan hjelpe oss med å skille listene fra hverandre.
Men standardavvikene skiller mellom listene. Dette svarer til det vi ser av grafene ovenfor – det er mindre standardavvik i kolonne B, C og F enn i A, D og E.
Siden vi vet at Alise samlet data over temperaturer, og at liste A var hennes data, kan vi konkludere med at listene med samme hovedtrekk, A, D og E, er Alises værdata.
Da er liste B, C og F Karls lister over vekta til tenåringer.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Elever kan kanskje tenke at gjennomsnittsverdien inneholder all den viktigste informasjonen om et datamateriale. Dataene i denne oppgaven er valgt slik at de seks listene med tall ikke kan skilles i to grupper ut fra gjennomsnittsverdier. Elevene må vurdere spredningen, de må bruke et eller flere spredningsmål. De kan tegne diagram (f.eks. linjediagram eller søylediagram) og få et bilde av hvor stor spredning dataene i hver liste har. Eller de kan bruke regnearket og finne gjennomsnittsverdi og standardavvik.
Mulig tilnærming
Introduser problemet, fortell hva Alise og Karl har arbeidet med, og hvilke data de har samlet. Tallene i de seks listene ser ganske like ut. Hvilke metoder fra statistikken kan elevene bruke for å avdekke hva som skiller listene i to ulike grupper?
La elevene diskutere i par hvilke metoder de tenker de kan bruke. Så kan dere samle forslagene på tavla. Forslagene kan inneholde både sentralmål og spredningsmål. Du bør la alle stå uten kommentarer, og la elevene selv få erfare at ikke alle forslagene viser forskjell på listene.
Så er det elevenes utfordring å finne ut hvilke lister som hører til Alise, og hvilke som hører til Karl. Elevene kan få regnearket som følger dette opplegget. Oppmuntre dem til å bruke det, for eksempel til å tegne grafer til hver liste. Og om de etterspør det, kan de få kommandoene til statistiske funksjoner som gjennomsnitt og standardavvik i regnearket.
Følg med på hvordan elevene arbeider, og merk deg gode strategier. Stopp klassen når det er tid for å dele erfaringer og løsninger. Sett av god tid til denne delen av arbeidet. Sørg for at ulike strategier blir presentert, og at de gode strategiene blir forstått. Elever som presenterer løsninger, må forklare hvilke egenskaper ved listene som gjorde at de kunne dele dem i to kategorier. Til slutt kan det bli en diskusjon om hvilke metoder som var effektive, og hvilke som var mindre effektive eller usikre, eller ikke var til hjelp for å skille listene fra hverandre.
Gode veiledningsspørsmål
- Hvilke statistiske teknikker kan være nyttige når du skal sammenligne datasett?
- Hvis du har tegnet diagram som representerer hver liste: Hva er hovedtrekkene i diagrammene? Er noen trekk like i alle? Kan noen trekk skille dem fra hverandre?
Mulig utvidelse
I aktiviteten "Datamatching" finnes det et tilsvarende problem der elevene skal sortere 16 lister med data i fire grupper.
Mulig støtte
Elevene kan tegne grafer i regnearket for hver av de seks listene (f.eks. søylediagram eller linjediagram). Be dem beskrive hovedtrekkene ved hver graf og finne noen likhetstrekk mellom grafene som gjør at de kan sorteres i to grupper, Alises og Karls værdata.
Ressursen er utviklet av NRICH