Venndiagrammoro
Aktivitet
Med venndiagram kan man representere alle mulige logiske sammenhenger mellom flere mengder.
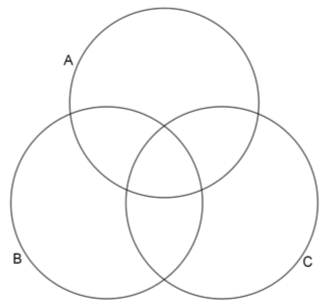
Figuren viser et venndiagram for de tre mengdene A, B og C. Det dannes 7 ulike områder eller delmengder når mengdene overlapper hverandre slik som på figuren.
Beskriv alle de syv områdene ved hjelp av følgende navn og symboler:
\(A, B, C, \overline{A}, \overline{B}, \overline{C}, \cup, \cap\)
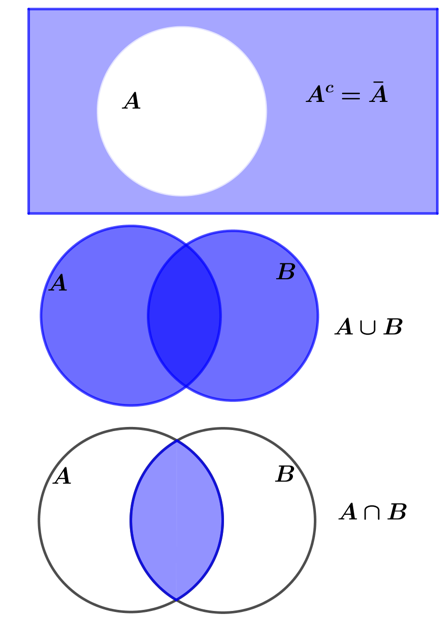
Merk: \(\overline{A}\) står for komplementærmengden til A, dvs. mengden av alt som ikke er i mengden A. En annen skrivemåte for komplementærmengden til A er \(A^c\).
Lag et venndiagram med fire mengder A, B, C og D.
Sørg for at diagrammet inneholder områder for alle mulige overlappinger mellom mengdene. Du må gjerne eksperimentere med hvordan diagrammet skal se ut for at det skal være enkelt å finne alle de ulike områdene som dannes. Hvor mange ulike områder finnes når fire ulike mengder overlapper mest mulig? Beskriv alle delmengdene med navn og symboler slik som i oppgaven med tre overlappende mengder.
Ekstra utfordring:
Hvis vi tenker oss mengder som er plassert slik at alle overlapper alle, men ingen overlapper hverandre helt: Kan du finne en måte å forutsi hvor mange områder/delmengder diagrammet blir delt opp i etter hvor mange mengder vi har?
Hvorfor blir det 7 ulike områder når tre menger overlapper på denne måten?
Hvor mange områder dannes hvis fire mengder overlapper i et venndiagram slik?
Og hvor mange blir det med et venndiagram av fem mengder?
Starthjelp
En kort repetisjon av symbolene du må bruke i denne oppgaven:
Løsning
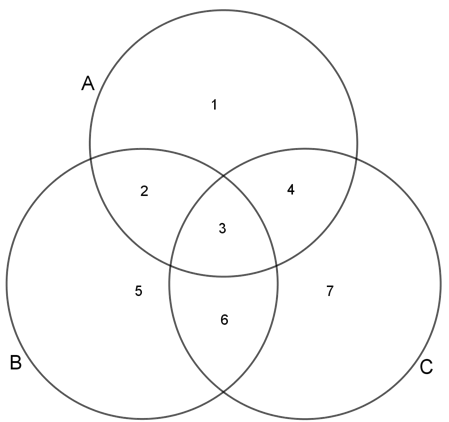
Vi nummererer de syv områdene:
\(1.\quad \overline{B}\cap{\overline{C}}\\ 2.\quad A\cap{B}\cap{\overline{C}}\\ 3.\quad A\cap{B}\cap{C}\\ 4.\quad A\cap{C}\cap{\overline{B}}\\ 5.\quad \overline{A}\cap{\overline{C}}\\ 6.\quad B\cap{C}\cap{\overline{A}}\\ 7.\quad \overline{A}\cap{\overline{B}} \)
Men hva med områder som 1 og 2 til sammen eller 2, 3 og 4 til sammen? Kan du gi disse navn ved hjelp av mengdenavnene og symbolene vi har brukt tidligere?
Et venndiagram kan tegnes med sirkler eller med andre former. Det eneste kravet i denne oppgaven er at de skal overlappe hverandre mest mulig, men ingen av dem må dekke noen av de andre mengdene helt.
For å lage et venndiagram med fire mengder, kan vi for eksempel tegne fire overlappende rektangler. Vi begynner med to overlappende rektangler, så må det tredje plasseres slik at det overlapper begge, men også har en del som er utenfor begge de to vi begynte med. Osv.
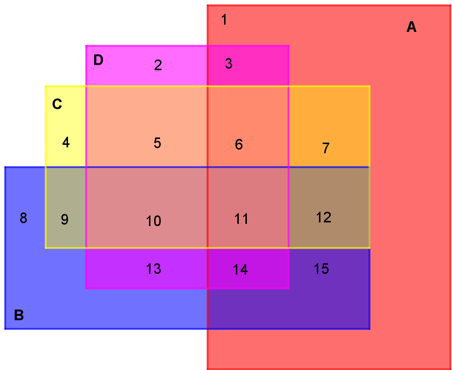
Vi har tegnet mengden A rød, mengden B blå, mengden C gul og mengden D rosa. Det blir 15 ulike områder. For eksempel blir:
\(1.\quad \overline{B}\cap{\overline{C}}\cap{\overline{D}}\\ 3.\quad A\cap{\overline{B}}\cap{\overline{C}}\cap{D}\\ 10.\quad \overline{A}\cap{B}\cap{C}\cap{D}\)
Kan du finne de øvrige selv?
Ekstra utfordring:
|
Antall mengder i venndiagrammet |
Antall områder/delmengder |
Mønster |
|
2 |
3 |
\(3 = 2^2-1\) |
|
3 |
7 |
\(3+3+1=2\cdot{(2^2-1)}+1=2^3-1\) |
|
4 |
15 |
\(7+7+1=2\cdot{(2^3-1)}+1=2^4-1\) |
|
5 |
31 |
\(15+15+1=2^5-1\) |
|
6 |
|
|
|
n |
|
\(2^n-1\) |
En måte å tenke på, er at vi ser for oss et diagram som starter med to mengder, og så legges en og en ny mengde på slik at det dannes så mange områder som mulig:
Vi starter med to mengder. Det blir ett overlappende område pluss to områder hvor de ikke overlapper.
Med tre mengder skal hvert av de tre områdene fra forrige diagram delvis overlappes av den nye mengden. I tillegg skal det være et område av den nye mengden som ikke overlappes av noen av de andre. Da blir det i alt 3 + 3 + 1 = 7 områder.
Med fire mengder skal de 7 områdene fra forrige diagram delvis overlappes av den nye mengden. I tillegg skal det være et område av den nye mengden som ikke overlappes av noen av de andre. Vi får 7 + 7 + 1 = 15 områder.
Med dette resonnementet vil 5 mengder danne 15 + 15 + 1 = 31 områder.
Det ser ut til at vi har et mønster, vi dobler antallet fra foregående diagram og legger til 1. Alle antallene ser ut til å være på formen \(2^n-1\). I tabellen ovenfor ser du av utregningene at antall områder følger denne regelen.
Ressursen er utviklet av NRICH