Kombiner to og to
Problem
På hvor mange måter kan du kombinere 2 av 6 elementer?
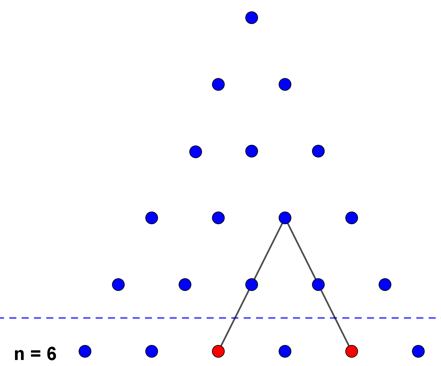
Bruk dette diagrammet til å bevise at antall ulike par som kan velges ut av 6 elementer, er
1 + 2 + 3 + 4 + 5
En vanlig skrivemåte for antall mulige måter å velge 2 elementer av 6, er binomialkoeffisienten \(\binom{6}{2}\). På kalkulatoren skrives det ofte 6C2.
Generaliser argumentet ditt, og vis at antall måter å trekke 2 elementer ut av en mengde på n elementer, er
\( \binom{n}{2}=1+2+3+...+(n-1)= \frac12n(n-1)\)
Ekstra utfordring:
Sammenlign denne formelen med definisjonen av \(\binom{n}{2}\), og vis at de uttrykker det samme.
Løsning
Diagrammet viser at hvert av punktene over den stiplede linja korresponderer med et unikt par av de 6 elementene som ligger under denne linja. Omvendt ser vi at hvert mulig par av de 6 elementene under streken korresponderer med ett og bare ett punkt i trekantdiagrammet over streken.
Diagrammet over den stiplede linja representerer trekanttallet T {5}. Antall mulige par vi kan trekke ut fra en mengde på 6 elementer, er lik det femte trekanttallet.
Tilsvarende kan vi tenke oss et diagram over det n-te trekanttallet. Nederste rad består av n elementer. På samme måte som når n = 6, kan vi alltid kombinere et par av elementer fra den nederste raden med et unikt element i mengden over streken. Og omvendt vil hvert element i trekantdiagrammet over streken korrespondere med et unikt par av elementer under streken. Det viser at antall måter å velge 2 ut av n elementer på, er
\( \binom{n}{2}=T_{n-1}=1+2+3+...+ (n-1)=\frac12n(n-1)\)
Definisjonen av binomialkoeffisienter:
\(\binom{n}{k}=\frac{n!}{k!(n-k)!} \quad hvis\quad 0\leq{k} \leq{n}\)
Definisjonen gir oss:
\(\binom{n}{2}=\frac{n!}{2!(n-2)!} =\frac{1\cdot2\cdot3...\cdot{(n-2)}\cdot{(n-1)}\cdot {n}}{1\cdot2\cdot1\cdot2\cdot3...\cdot(n-2)}=\frac{(n-1)n}{2}=T_{n-1}\)
Så vi har altså vist at \(\binom{n}{2}=T_{n-1}\).
Ressursen er utviklet av NRICH