Overbooking
Aktivitet
Et flyselskap har et fly med 400 seter. Sannsynligheten for at en passasjer som har kjøpt billett, møter opp og blir med flyet, er 0,95.
Hvis flyselskapet selger 400 billetter, hvor mange tomme seter kan vi da forvente at det blir?
Flyselskapet har rutiner for å selge mer enn 400 billetter til en flyreise.
Hvor mange billetter kan selskapet selge hvis de ikke vil måtte avvise passasjerer som har billett og har møtt opp, i mer enn høyst ca. 2 prosent av avgangene?
Starthjelp
- Hva er sannsynligheten for «å lykkes»?
- Hva er forventningsverdi, varians og standardavvik for fordelingen?
- Du kan bruke sannsynlighetskalkulatoren i GeoGebra.
Løsning
Passasjerene som har kjøpt billetter til en flyavgang, møter enten opp eller ikke. La X være en stokastisk variabel for antall passasjerer som møter opp. Da er X binomisk fordelt med sannsynlighet for «å lykkes», p = 0,95. Og la n være antall solgte billetter. Sannsynlighetsfordelingen er:
\(P(x;n,p)=\binom {n}x p^x\cdot(1-p)^{n-x},\text { } x=0, 1, 2, ..., n\)
Forventningsverdien til den binomiske fordelingen når n = 400, er \(E(X)=np=400\cdot0,95=380\), variansen er \(\sigma^2=np(1-p)= 400\cdot0,95\cdot0,05=19\), og standardavviket er \( \sigma =\sqrt{19}\approx4,36\).
Hvis flyselskapet selger 400 billetter, er forventningsverdien 380, det vil si at en kan forvente at det blir 20 tomme seter på flyturen.
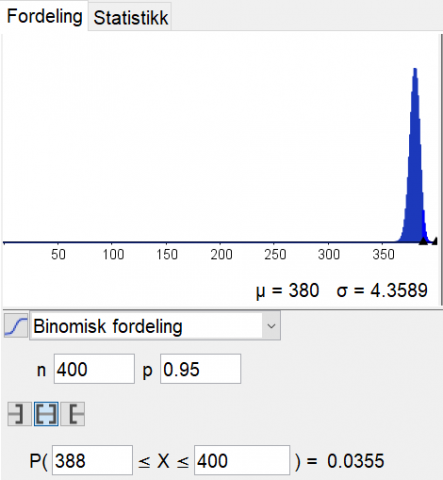
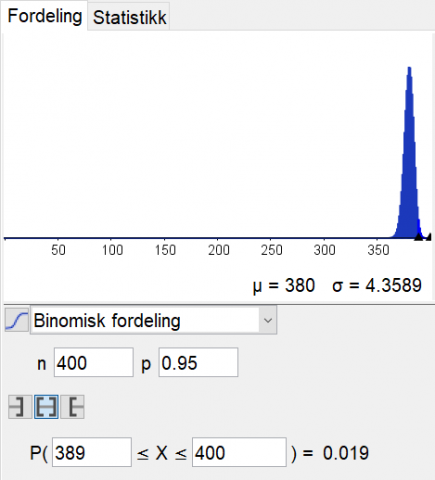
Vi kan for eksempel bruke sannsynlighetskalkulatoren i GeoGebra. Der kan vi ved å prøve oss fram finne at sannsynligheten for at det møter opp mellom 388 og 400 passasjerer som har kjøpt billett, er 0,0355, mens sannsynligheten for at det møter opp mellom 389 og 400 passasjerer, er 0,019. Så hvis flyselskapet selger inntil 400 – 389 = 11 billetter ekstra, er sannsynligheten høyst 2 prosent for at alle møter opp og noen må stå igjen.
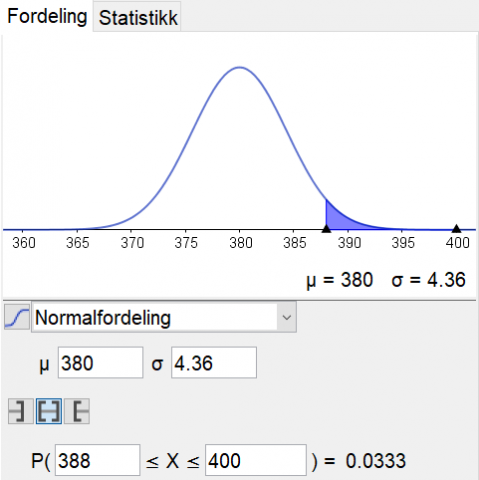
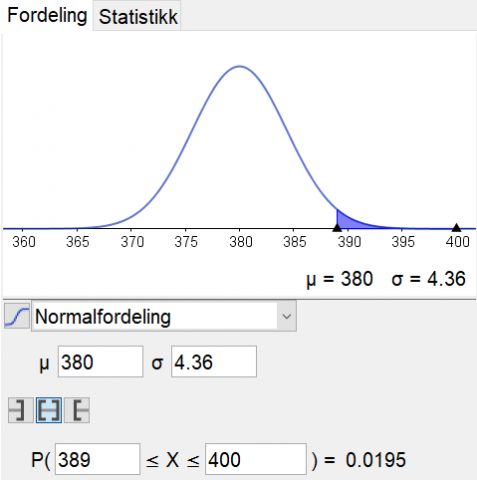
Siden \(np=400\cdot0,95=380\geq 5\) og \(n(1-p)=400\cdot0,05=20\geq 5\), er materialet i den bionomiske fordelingen stort nok til at det kan tilnærmes til en normalfordeling med samme forventningsverdi og standardavvik. Vi kunne ha brukt sannsynlighetskalkulatoren for normalfordeling på tilsvarende måte og kommet til det samme resultatet:
Selskapet kan selge inntil 411 billetter hvis de ikke vil måtte avvise passasjerer som har billett og har møtt opp, i mer enn høyst ca. 2 prosent av avgangene.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven er en øving i å bruke normalfordeling som tilnærming til en binomisk fordeling.
Problemet er ikke som i de fleste oppgaver der en blir bedt om å finne sannsynligheten for at et utfall ligger innenfor et bestemt intervall, altså sannsynligheten for at et visst antall passasjerer vil møte opp til en flyavgang. Her er problemet omvendt, og løsningen involverer at en må prøve og feile litt for å finne løsningen.
Ressursen er utviklet av NRICH