A4 Brøkaddisjon
Aktivitet
To elever arbeider sammen. Start med et A4-ark og en saks hver. Gjør aktiviteten og sammenlikn det dere har laget.
Hele A4-arket representerer 1 hel.
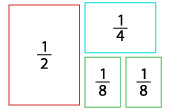
Brett arket i to like rektangler. Klipp langs brettelinja. Da kan du få deler som likner de to rektanglene under. Hvert av disse rektanglene representerer \(\frac12\).
Brett et av rektanglene og klipp det i to mindre rektangler på samme måte som du gjorde med det forrige. Du har nå to nye rektangler som hver for seg representerer \(\frac14\), som de blå rektanglene nedenfor.
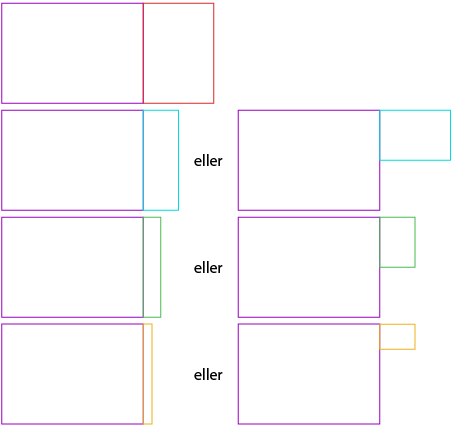
Avhengig av hvordan du valgte å dele rektangelet i to, kan \(\frac14\)-rektanglene dine se annerledes ut enn dette. De kan være lange og tynne, som rektanglene nedenfor.
Nå tar du et av \(\frac14\)-rektanglene dine, bretter og klipper de i to. Da får du to nye rektangler som begge representerer \(\frac18\), som de grønne rektanglene nedenfor.
Når du halverer et av de grønne rektanglene dine, får du to \(\frac1{16}\)-rektangler, som det oransje nedenfor. Kast et av \(\frac1{16}\)-rektanglene, slik at du har ett rektangel av hver størrelse.
Sammenlikn rektanglene dine med en annen elev. Ser de like ut? Er de ulike dem på figuren ovenfor?
Tenk deg at du har laget \(\frac12\)-rektangelet ditt på samme måte som det røde rektangelet ovenfor, men at du har klippet de andre rektanglene dine slik at de ble lange og smale. Da kan rektanglene dine se slik ut:
Finnes det andre rektangler du kunne ha valgt?
Du trenger fire A4-ark. Legg et ark inntil hver av brøkdelene dine. Husk at hele A4-arket regnes som «en hel». Da får du kombinasjoner som likner på dem nedenfor. Alle disse figurene består av en heltallsdel (A4-arket) og en brøkdel. Et tall som består av en heltallsdel og en brøkdel, er et blandet tall.
Kan du finne ut hvilket blandet tall som representerer hver av figurene over?
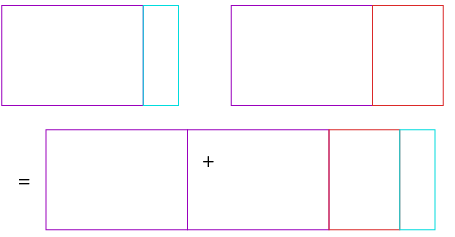
Sett en av blandet-tall-figurene dine sammen med en som medeleven din har laget. Skriv ned addisjonsstykket og svaret.
Eksemplet nedenfor vil gi regnestykket \(1\frac14+1\frac12=2\frac34\).
Hvor mange forskjellige addisjonstallsetninger kan du lage?
Du kan også prøve en subtraksjonsversjon av denne oppgaven.
Lærerveiledning
Hvorfor jobbe med dette problemet?
Denne aktiviteten hjelper elevene med å utvikle brøkbegrepet og begynne å addere brøker med lik nevner og nevnere som er multipler av samme tall. Aktiviteten legger opp til utforsking og resonnement rundt egenskaper ved brøker.
Mulig tilnærming
Begynn med et stort stykke papir, og del det i brøkdeler ved gjentatt halvering (som i første del av aktiviteten). Diskuter størrelsen på delene du lager, med elevene. Be elevene foreslå hvordan du kan dele papiret i to like rektangler (halvdeler). Det kan gjøres på to måter i hvert steg!
Fest noen av delene på et nytt stykke papir (som i den andre delen av aktiviteten), og be elevene beskrive de «nye» delene (1 1/2, 1 1/4, 1 1/8 og 1 1/16).
Ved å arbeide i par kan elevene gjenta aktiviteten med sine egne papirlapper. Deretter kan de gjøre addisjoner ved å bruke sine egne brøker, og skrive ned så mange tallsetninger de kan.
Gode veiledningsspørsmål
- Fortell meg om størrelsen på dette rektangelet.
- Hvordan adderer du disse to?
- Hvordan vet du at løsningene dine er riktige?
- Kunne du ha valgt et annet rektangel for å representere den brøken?
- Finnes det andre måter å addere brøker på?
Mulig utvidelse av oppgaven
Når elevene har laget 1 1/2, 1 1/4, 1 1/8 og 1 1/16, kan de lage 1 3/4, 1 3/8 og 1 3/16. Da kan elevene se hvor mange addisjonstallsetninger de kan lage, inkludert disse. De kan også lage ulike representasjoner for samme addisjoner ved å velge rektangler med forskjellige former som representerer den samme brøken.
Mulig støtte
Elevene kan få klippe ut brøkene av ark der linjene er markert (kopioriginal).
Send inn elevsvar
Ressursen er utviklet av NRICH