Hvem er hvem
Aktivitet
Vi kan representere en gruppe venner ved å tegne en type diagram.
Hver sirkel representerer en person.
En linje kobler sammen to sirkler hvis, og bare hvis, de to personene er venner.
Oppgave 1
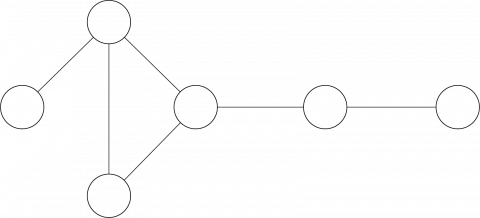
Nedenfor ser du et diagram som representerer en gruppe venner.
Kan du finne ut hvem som er hvem ved å bruke ledetrådene nedenfor?
- Allan har 3 venner, Børre, Charlie og Daniel.
- Børre og Eddie er begge venner med Charlie.
- Eddie er den eneste vennen til Frank.
Oppgave 2
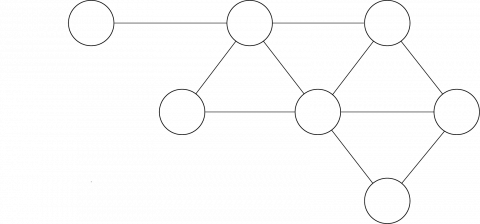
Her et annet nettverk av venner.
Prøv igjen å bruke ledetrådene nedenfor til å finne ut hvem som er hvem.
- Bella og Caroline er venner.
- Emilie og Caroline er ikke venner.
- Bella er den eneste vennen til Frida.
- Anne har flest venner av alle sammen.
- Dina har tre venner.
- Gina og Dina er ikke venner.
- Emilie har to venner.
Starthjelp
- Noen av opplysningene gjør at noen personer kan plasseres bare på ett sted i diagrammet.
- Noen opplysninger må brukes i kombinasjon med andre.
- Prøv deg fram og se! hvis det du prøver, ender med en motsigelse, må du prøve noe annerdeles.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette er en oppgave hvor elevene må finne egne løsningsstrategier. Ved å høre andres løsninger og diskutere, kan de også se at noen strategier er mer effektive enn andre.
Strategien i begge disse oppgavene er å først finne sirklene som hver enkelt kan høre til i, og så prøve og feile ved å sjekke at alle opplysningene er oppfylt. Det er viktig å lese igjennom alle ledetrådene før man begynner å lete etter løsning.
Kopieringsoriginal til oppgaven finnes her.
Gode veiledningsspørsmål
- Er det noen av ledetrådene som gjør det enkelt å plassere en person?
- Er det noen av ledetrådene som er slik at en person har bare et begrenset antall mulige plasseringer? Kanskje må du prøve deg fram med en av de mulige plasseringene om gangen.
- Har hver oppgave en unik løsning?
- Var det noen ledetråder du ikke trengte å bruke?
- Hvis du nummererer hver sirkel med det antallet venner personen har, og summerer alle tallene, hva kan du si om svaret? Kan du forklare hvorfor?
- Når du mener du ha løst oppgaven: Gå nøye igjennom ledetrådene og kontroller at alle kravene er oppfylt!
- Kan du lage et lignende problem med fem venner, der noen personer har mer enn to venner, med en unik løsning?
Send inn elevsvar
Ressursen er utviklet av NRICH