Mønsteret som vokser

Stikkord: Mønster Generalisering

Problem

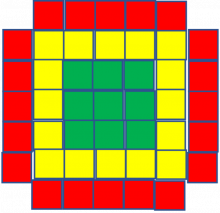
Figuren nedenfor viser de tre første figurene i et mønster der hver figur har et kvadratisk hull i midten.

Thumbnail

Hvor mange blå kvadrater trengs for å lage den tiende figuren i mønsteret?

Tilleggsspørsmål:

  • Hvordan ser du at mønsteret vokser?
  • Hvordan ser du at figurene er bygd opp?
  • Kan du regne ut hvor mange blå kvadrater som trengs til et hvilket som helst figurnummer (for eksempel figur 24)? Forklar hvordan du tenker og hvorfor det blir riktig.
  • Kan du forklare hvordan du kan finne antallet for neste figur hvis du kjenner den forrige? Kan du lage en figur som viser hvordan du tenker?

Løsning

Løsningsforslag 1-3

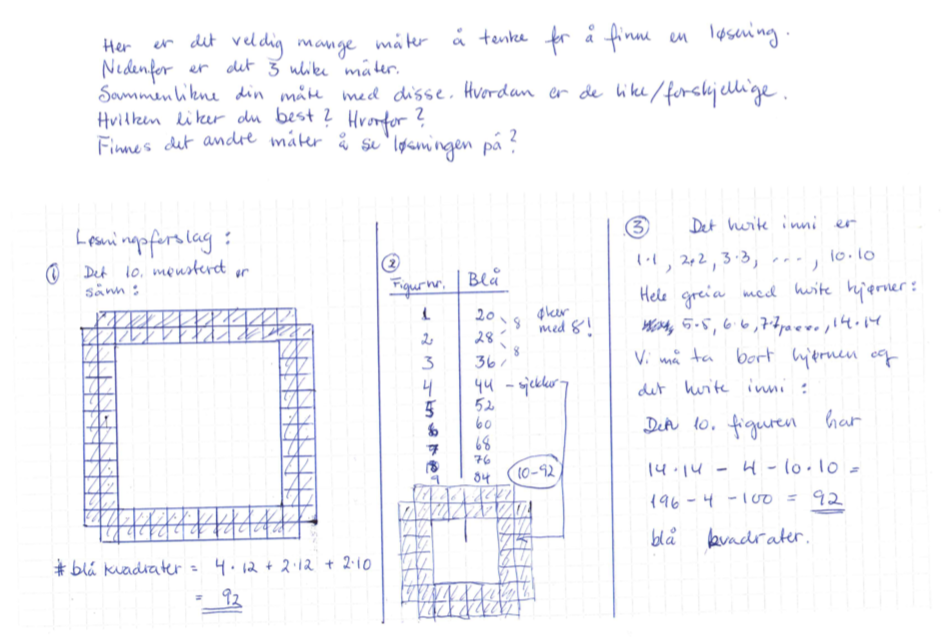
løsning 188

Løsningsforslag 4-6

Anders Ness Nilsen – lærer ved Hammer skole – har sendt oss disse tre løsingsforslagene:

Løsningsforslag 4
  1. Du finner antall klosser i hele kvadratet først. Sidene i kvadratet er 4 større enn figurnummeret.
  2. Du trekker fra det røde kvadratet. Sidelengden er lik figurnummeret.
  3. Du trekker fra de fire hjørnene

\(F_n=(n+4)^2-n^2-4\)​ 

 
Løsningsforslag 5
  1. Du ser at for hver figur vokser det med en arm i midten (to brikker). Antall armer er lik figurnummeret.
  2. Du legger til de tre gule boksene, som det er fire av.

\(F_n=2n\cdot4 +4\cdot3\)

 
Løsningsforslag 6
  1. De ytterste brikkene (røde) er to mer enn figurnummeret.
  2. Du finner ut hvor mange brikker det er i det gule kvadratet.
  3. Du trekker fra det grønne kvadratet.
  4. Punkt 2 og 3 kan du gjøre på forskjellige måter (videreføring av Rammeproblemet).

\(F_n=4(n+2)+(n+2)^2-n^2\)

Ressursen er utviklet av NRICH

8,9