Trekantet hjul
Problem
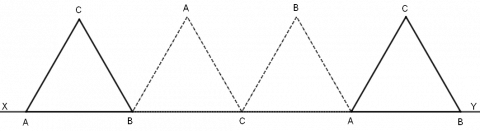
Den likesidede trekanten ABC har sidelengde 1, og AB ligger på linja XY.
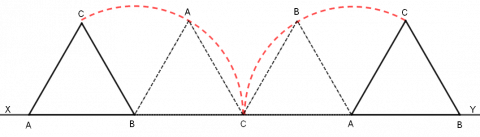
Trekanten roteres med klokka om punktet B, helt til BC ligger på XY. Så roteres den på samme måte om C, og til slutt roteres den om A, slik figuren viser.
Hvor lang er veien som punktet C følger gjennom denne serien av rotasjoner?
Løsning
Ved den første rotasjonen beveger punktet C seg i en bue på 120° med radius 1. Det er en tredel av en sirkelomkrets med radius 1.
Ved den andre rotasjonen ligger punktet C i ro, og ved den tredje rotasjonen beveger punktet seg igjen over en bue på 120°.
Punkt C beveger seg en strekning på \(\frac23 \cdot 2\pi \cdot 1=\frac {4\pi}{3}\)
Ressursen er utviklet av NRICH
9