Konstruer trekanter!
Aktivitet
Bruk en 10-sidet terning eller noe annet som kan gi tre tilfeldig valgte tall mellom 1 og 10 (f.eks. kort med tall 1–10 fra en kortstokk, men legg tilbake kortet for hver trekking).
Når dere har fått tre tall, skal dere konstruere en trekant med disse tallene som sidelengder.
Hvis du ikke er sikker på hvordan du konstruerer en trekant ved hjelp av linjal og passer, kan du se på denne videoen.
Gjør noen flere forsøk med å konstruere trekanter ut fra tre tilfeldige tall mellom 1 og 10.
Hva legger du merke til?
Her er noen spørsmål som du kan tenke over:
• Når du har fått tre tall som skal være lengden på sidekantene, kan du da konstruere flere ulike trekanter?
• Er det alltid mulig å konstruere trekanter ut fra tallene du får?
• Er det noen rask måte for å avgjøre om det vil være mulig å konstruere en trekant med tre gitte tall?
Her er et spill du kan spille alene:
Begynn med 10 poeng. Kast terningen tre ganger. Hvis du kan bruke tallene til å konstruere en trekant, får du ett poeng, hvis ikke må du trekke fra et poeng. Hvis du får 20 poeng, har du vunnet spillet, hvis du får 0 poeng, har du tapt.
Hvilket resultat er mest sannsynlig?
Her er et spill du kan spille sammen med en annen:
Spiller A velger en hel lengde mellom 1 cm og 10 cm. Spiller B kaster så terning to ganger, slik at dere får lengden på de to neste sidene. Hvis det er mulig å konstruere en trekant med disse tallene, vinner B. Hvis ikke, vinner A.
Er det noen lengder det er smart av A å velge?
Er dette et rettferdig spill?
Aktiviteten kan utvides med at dere prøver å konstruere en firkant med fire tilfeldig valgte tall mellom 1 og 10.
Løsning
Med en gitt kombinasjon av tre tall kan du ikke konstruere flere ulike trekanter. Du kan konstruere trekanter som ser forskjellige ut, avhengig av hvilken lengde du velger som grunnlinje, men alle trekantene du konstruerer, vil ha lik form, de vil bare være litt forskjellig plassert eller speilvendt.
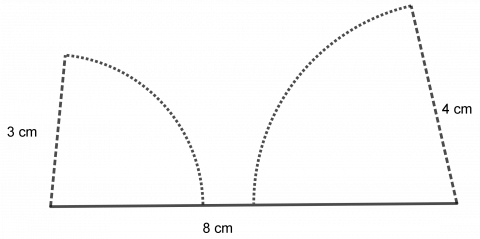
Det er ikke alle kombinasjoner av tre tall som gjør det mulig å konstruere en trekant, for eksempel hvis du får tallene 8, 3 og 4:
Løsningen er at summen av de to korteste sidene må bli større enn den lengste.
Hvis den lengste siden er 8 cm, må summen av de to andre være større enn 8 cm.
Vi kan lage en oversikt over alle kombinasjoner av tall som sammen med 8 kan danne en trekant:
8 10 10
8 10 9
8 10 8
8 10 7
8 10 6
8 10 5
8 10 4
8 10 3
OBS! Når 10 er det største tallet, må summen av de to andre være større enn 10.
8 9 9
8 9 8
8 9 7
8 9 6
8 9 5
8 9 4
8 9 3
8 9 2
OBS! Når 9 det største tallet, må summen av de to andre være større enn 9.
8 8 8 Herfra er 8 det største tallet.
8 8 7
8 8 6
8 8 5
8 8 4
8 8 3
8 8 2
8 8 1
8 7 7
8 7 6
8 7 5
8 7 4
8 7 3
8 7 2
8 6 6
8 6 5
8 6 4
8 6 3
8 5 5
8 5 4
På tilsvarende måte kan vi sette opp alle mulige kombinasjoner med alle de mulige sidelengdene.
Hvilke kombinasjoner er det flest av?
Det er flere kombinasjoner som ikke gir trekant enn som gir trekant. Så i det første spillet er det mer sannsynlig å ende med 0 poeng enn med 20 poeng.
Hvis spiller A ønsker at B ikke skal vinne, bør A velge 1 cm. Det er svært få kombinasjoner som har en side på 1 cm, bare likebeinte trekanter: 10-10-1, 9-9-1 osv. Så hvis A velger 1 cm, må B få to like tall for å vinne. Dette er altså ikke et rettferdig spill.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven gir et spennende utgangspunkt for å konstruere trekanter med linjal og passer. Elevene får også arbeide med det som ligger i begrepene «umulige trekanter» og kongruens. Oppgaven utfordrer elevene til å tenke på permutasjoner, kombinasjoner og sannsynlighet.
Mulig tilnærming
Du må forsikre deg om at elevene vet hvordan de skal konstruere en trekant, når de kjenner de tre sidelengdene. De trenger blanke ark (ikke ruter eller linjer), linjal og passer. De trenger også 10-sidede terninger eller noe annet som kan gi tilfeldige tall mellom 1 og 10 (f.eks. kortene 1–10 fra en kortstokk). Det er viktig at elevene konstruerer, for hvis de bare lager hjelpefigurer og setter på mål, er det fort gjort å bli lurt til å tro at en «umulig» konstruksjon er mulig.
La elevene arbeide i par.
«Hvert par bestemmer hvem som skal begynne med å generere tre tilfeldige tall mellom 1 og 10. Så skal den andre konstruere en trekant med disse tre tallene som sidelengder. Dere får ett poeng for hver trekant dere klarer å konstruere. Når den første oppgaven er løst, skal dere bytte roller. Den som har flest poeng etter fem runder, har vunnet. Dere må notere poengene etter hvert.»
La elevene arbeide med denne oppgaven en stund. Så kan du samle klassen og høre hvilke erfaringer de har gjort, om det er noe spesielt de har funnet ut underveis, eller om det er en sammenheng de tror kanskje må gjelde.
Hvis ingen har kommentarer, kan du for eksempel spørre:
«Har noen eksempler på at de kan konstruere flere ulike trekanter med samme tall?» Her kan det bli en diskusjon om kongruens og hva det betyr at to trekanter er like eller ulike.
«Har noen sett eksempler på tall som det ikke gikk an å lage trekanter av?» Del tavla i to, og skriv opp eksempler som elevene har på trekanter som kan konstrueres, og trekanter som ikke kan konstrueres.
«Diskutere med partnerne deres, og prøv å finne en forklaring på at løsningene på den ene siden kan konstrueres, mens trekantene på den andre siden ikke kan konstrueres.»
«Snart vil jeg gi dere tre store tall, og dere må kunne forklare meg om jeg kan konstruere en trekant med disse tallene eller ikke, og hvorfor eller hvorfor ikke.»
Etter at elevene har fått litt tid til å diskutere, kan du samle dem igjen og gi dem tre tall, for eksempel {35, 43, 79} eller {12, 23, 32}. La dem tenke seg litt om, og la så noen forklare om disse tallene kan være sidelengder i en trekant eller ikke. Til slutt må dere i fellesskap konkludere med en klar regel for hvordan en kan avgjøre om en trekant kan konstrueres eller ikke.
Å spille og analysere disse tre spillene kan være en passende oppfølging:
- Spiller A velger en hel lengde mellom 1 cm og 10 cm. Spiller B kaster så terningen to ganger, slik at dere får lengden på de to neste sidene. Hvis det er mulig å konstruere en trekant med disse tallene, vinner B. Hvis ikke, vinner A.
Er det noen lengder det er smart av A å velge? - Spiller A kaster terning og får et helt tall mellom 1 og 10. Spiller B kaster så terningen to ganger, og nå har dere fått lengden på alle tre sidene. Hvis dere kan konstruere en trekant med tallene, får B ett poeng, hvis ikke får A ett poeng. Førstemann til 20 poeng har vunnet.
Er dette et rettferdig spill? - Et solospill: Begynn med 10 poeng. Kast terningen tre ganger. Hvis du kan bruke tallene til å konstruere en trekant, får du ett poeng, hvis ikke må du trekke fra ett poeng. Hvis du får 20 poeng, har du vunnet spillet, hvis du får 0 poeng, har du tapt.
Hvilket resultat er mest sannsynlig?
Mulig utvidelse
Elevene kan utfordres til å avgjøre hva slags vinkler trekanten har, bare ved å se på sidelengdene.
Kan dere forutsi om trekanten er rettvinklet, har spisse vinkler eller har stumpe vinkler, bare ved å se på tallene?
Kan dere se på tallene og avgjøre om noen trekanter blir likebeint eller likesidet?
Elevene kan også undersøke hva som skjer hvis de bruker fire tilfeldig valgte tall mellom 1 og 10, og prøver å konstruere firkanter. De kan oppmuntres til å gjøre undersøkelsene ved å tegne i GeoGebra.
Mulig støtte
Hvis dere ønsker å gå nærmere inn på kombinatorikken og å få en oversikt over alle mulige kombinasjoner, kan det være litt mer oversiktlig å bruke en 6-sidet terning. Dere kan organisere og analysere alternativene og finne sannsynligheten for å få en trekant eller ikke, og sannsynligheten for å få en rettvinklet, likebeint eller likesidet trekant.
Ressursen er utviklet av NRICH