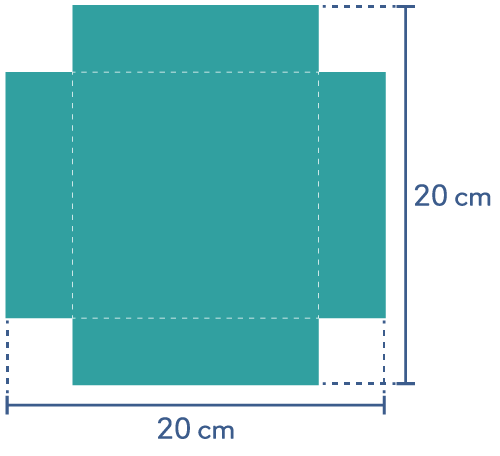
Prismeutfordring

Hvorfor arbeide med denne oppgaven?

Dette er et godt eksempel på en oppgave med lav inngangsterskel og stor takhøyde, som kan løses på forskjellige måter. Oppgaven legger til rette for visualisering, 2D-representasjon av 3D-former og volumberegninger, og elevene kan introduseres for tanken om å finne den optimale løsningen – et viktig poeng i matematikk. Siden det er mange måter å angripe utfordringen på, kan de erfare nye måter å resonnere matematisk på, gjennom numeriske, algebraiske og grafiske representasjoner. Noen kan også finne en sammenheng som kan uttrykkes som en funksjon.

Mulig tilnærming

Del ut kopioriginalen som inneholder oppgaveteksten.

«Tenk deg at du har et kvadratisk ark på 20 cm x 20 cm. Se for deg at du klipper vekk kvadrater med sidelengde 5 cm i hvert hjørne, og bretter opp sidene slik at du får en eske uten lokk. Hva blir målene på denne esken? Diskuter med en medelev. Hva blir volumet av esken?»
La elevene snakke litt sammen før dere diskuterer i plenum og blir enige om målene og volumet av en slik eske. Elevene skal forklare hvordan de fant målene og volumet. Det kan være lurt å bruke en tabell eller å tegne opp den ferdige esken på tavlen.

«Kan vi lage en eske med større volum?»

La elevene få litt tid til å arbeide sammen i par for å utforske hvordan kvadrater med forskjellige størrelser påvirker volumet av esken. Deretter kan du samle inn resultater i en tabell eller et regneark.

«Hva er det største volumet vi har funnet så langt? Kan vi finne noe enda større?»

Be elevene om å se etter og kommentere mønstre de ser i resultatene, og foreslå metoder som kan føre til den optimale løsningen.

• Prøv og feil, med eller uten kalkulator.
• Bruk et regneark og en formel som beregner volumet av en eske med en gitt størrelse på kvadratene som klippes vekk.
• Finn en formel eller funksjon, og bruk en graftegner til å finne den maksimale verdien / den optimale løsningen.

Oppfordre noen elever til å prøve de forskjellige metodene. Etter hvert samler du klassen slik at dere kan sammenligne og diskutere resultatene.

Når elevene har funnet den optimale løsningen for et kvadrat på 20 cm x 20 cm, kan du gi forskjellige grupper hvert sitt utgangspunkt. Én gruppe kan for eksempel begynne med et kvadrat på 10 cm x 10 cm, en annen med et på 30 cm x 30 cm, osv. Kan elevene bruke en av metodene for å finne den mest optimale løsningen for det nye kvadratet?

Til slutt samler du informasjonen om hvilke utklippete kvadrater som gir størst volum for de forskjellige utgangspunktene, og ber elevene om å se etter et generelt mønster som vil fungere for et hvilket som helst utgangspunkt.

Gode veiledningsspørsmål

• Hvordan kan du være sikker på at du har funnet det størst mulige volumet?
• Kan du overbevise noen andre?

Mulig utvidelse

I stedet for å begynne med kvadratiske ark kan elevene undersøke rektangulære utgangspunkt. For å gjøre mønsterspottingen enklere kan det være lurt å organisere dette, for eksempel ved å gi gruppene sett med rektangler der lengden er dobbelt så lang som bredden, tre ganger så lang, fire ganger så lang, osv.

Elevene kan bruke algebra til å representere forholdene de finner, og hvis de har kjennskap til funksjoner, kan de bruke det til å finne det størst mulige volumet.

Mulig støtte

Gi elevene ruteark på 20 cm x 20 cm, og la dem lage esker med forskjellige størrelse. Oppfordre dem til å arbeide systematisk og holde orden på resultatene sine.