Noen ganger mister vi ting
Aktivitet
Noen ganger sier folk: «Det handler bare om å være ryddig!» Men av og til har ting det med å forsvinne likevel!
Ti veldig nyttige ting kan brukes til mye forskjellig. Vi bruker tall til å telle med, og også til å utforske matematikk.
Men hva ville skje om vi mistet ett av tallene, eller sifrene som vi også kaller dem? Vi kunne for eksempel ha mistet alle niere. Hvis menneskene, for lenge siden, hadde bestemt seg for å telle med niere i stedet for tiere, måtte vi telle slik:
1 2 3 4 5 6 7 8
Og så måtte vi si «en nier og ingen enere», og da ville vi hatt 10.
Men denne 10 ville IKKE bli lest som ordet ti – i stedet ville vi sagt NI.
(Kanskje du har lagt merke til at før vi mistet sifferet 9, ville vi sagt TI når vi så 10, men vi hadde ikke et eget symbol for TI.)
Nå har vi altså mistet sifferet for NI, så vi må bruke 10 for NI.
Hvis vi teller videre, blir det slik:
Hvis vi hadde talt videre, ville vi etter hvert ha kommet til:
71 – sju niere, en
Og hvis vi teller litt til:
121 – en (ni niere), to niere, en
Prøv å telle litt videre selv, og skriv ned hvordan man kan si tallene, slik tabellen over viser.
Nå skal vi se på multiplikasjonstabellen. Prøv å skrive inn tallene slik de er når vi har mistet 9-tallet.
Blir det vanskelig, kan du ta en titt på bildet som ligger under Starthjelp.
Etter at du har fylt ut multiplikasjonstabellen, kan du lete etter og utforske mønster. Se på sammenhengene mellom ulike tall. Husk å snakke om tallene på den nye måten, slik at det siste tallet i tabellen er «sju niere og en» (i stedet for «sju tiere og en», eller syttien).
Etter å ha utforsket multiplikasjonstabellen kan du selv lage spørsmål og finne svar på dem. Et eksempel: «Hvordan det ville bli hvis vi hadde mistet 8 i tillegg til 9?»
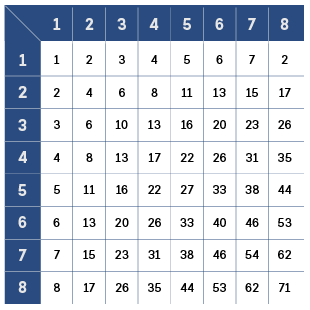
Starthjelp
Her ser du den ferdig utfylte multiplikasjonstabellen. Kanskje trenger du bare å se på deler av den for å kunne fortsette på egen hånd.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten kan brukes til å introdusere andre tallsystemer. Arbeid med andre tallsystemer kan gi elevene bedre forståelse av det som skjer når vi arbeider i vårt «eget» tallsystem, titallssystemet. I tillegg er aktiviteten fin å bruke til utforsking, og man kan finne mange mønstre i multiplikasjonstabellen. Elevene bør også oppfordres til å begrunne hvorfor mønstrene oppstår.
Mulig tilnærming
Du kan introdusere aktiviteten med romvesener som har ni fingre i stedet for ti. Så kan du gå gjennom enkel telling som om du var dette ni-fingrede romvesenet. Elevene kan være med på å telle.
Når dere har gjort tellingen sammen, kan du vise måten å skrive tallene på, før elevene kan fortsette selv, gjerne i par.
Mulig støtte
For noen elever kan det være nyttig å ha tilgang til konkreter som viser tallet 9 fysisk, for eksempel et lekeromvesen med ni fingre.
Ressursen er utviklet av NRICH