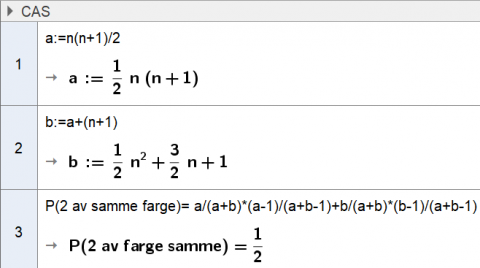Hvem må ta oppvasken?
Aktivitet
To jenter, Siri og Anna, deler hybel. De er stadig uenige om hvem som skal ta oppvasken, så de vil løse problemet ved trekning. De legger fire brikker i en skål, to røde og to blå, og bestemmer seg for at de skal trekke to brikker. Hvis de trekker to brikker med ulike farger, skal Siri vaske opp, og hvis de trekker to brikker med samme farge, skal Anna vaske opp.
- Er dette en rettferdig ordning? Vil de måtte vaske opp omtrent like mange ganger hver? Forklar hvordan du har tenkt.
- Hvis det ikke er rettferdig, hvor mange brikker i hver farge må de legge i skåla for at trekningen skal bli rettferdig?
- Er det mer enn én måte å kombinere røde og blå brikker på slik at trekningen gir Siri og Anna omtrent like mange oppvasker hver?
Starthjelp
- Lag et sett med brikker, og trekk flere ganger, slik Siri og Anna gjorde.
- Prøv dere fram med å variere antallet av røde og blå brikker.
- Hvor mange forsøk mener du må gjøres før en kan avgjøre om en kombinasjon av brikker er rettferdig?
- Har du en måte å systematisere kombinasjonene av røde og blå brikker på?
- Kan du finne sannsynlighetene for å trekke to av samme farge eller to med ulike farger?
Løsning
Ordningen Siri og Anna kom fram til, var ikke rettferdig. Vi kan vise det på flere måter. Legg merke til de ulike måtene å forklare det på, og prøv å forstå alle.
1. Kombinatorikk, uordnede utvalg:
Vi kan gi hver brikke et nummer og skrive opp alle mulige resultater av trekninger:
| 1, 2 | 2, 3 |
| 1, 3 | 2, 4 |
| 1, 4 | 3, 4 |
To av seks utfall er brikker med samme farge.
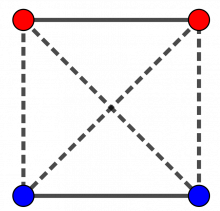
Vi kan også lage en tegning av brikkene så vi er sikre på å få med alle mulige kombinasjoner. Vi lar stiplet linje forbinde to brikker av ulik farge og heltrukken linje to brikker av samme farge. Resultatet blir det samme:
Det er fire forbindelseslinjer mellom to brikker av ulik farge og to forbindelseslinjer mellom to av samme farge. Det blir to utfall med to like farger og fire utfall med to ulike farger, så Siri kan regne med å måtte ta dobbelt så mange oppvasker som Anna.
2. Kombinatorikk, ordnede utvalg:
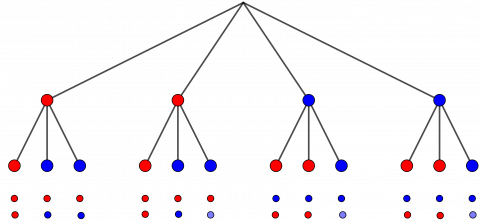
Vi kan tegne et valgtre eller lage en tabell for å få oversikt over alle mulige kombinasjoner:
| R | R | B | B | |
| R | - | RR | RB | RB |
| R | RR | - | RB | RB |
| B | BR | BR | - | BB |
| B | BR | BR | BB | - |
Vi ser at det er 12 mulige utfall, og 4 av dem har to like farger, mens 8 har to ulike farger. Forholdet blir altså det samme som i forrige løsning: Siri må vaske opp dobbelt så mange ganger som Anna.
3. Sannsynlighet:
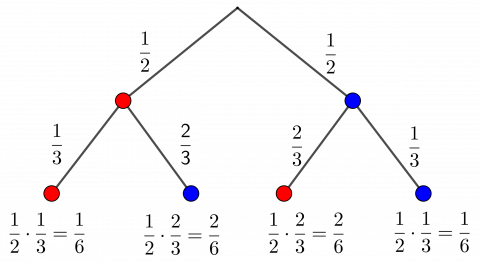
Vi kan tegne et valgtre eller sette opp en utregning med sannsynligheter for å vise det samme som ovenfor:
\(\text{P(to av samme farge) = P(rød og rød) + P(blå og blå)}\)
\(=\frac12\cdot\frac13+\frac12\cdot\frac13=\frac26=\frac13\)
\(\text{Da blir P(to av ulik farge) = 1 - P(to av samme farge)}= 1-\frac13=\frac23\).
Vi prøver med andre antall av brikker i to farger
- Vi kan prøve med to røde og fire blå brikker:
P(to av samme farge) = P(to røde) + P(to blå)
\(=\frac26\cdot\frac15+\frac46\cdot\frac35=\frac2{30}+\frac{12}{30}=\frac{14}{30}=\frac7{15}\).
Dette er ikke rettferdig, for sannsynligheten må bli \(\frac12\) for at det skal være like sannsynlig å trekke to like som to ulike. Men det ble mye nærmere, så det var mer rettferdig enn med to brikker av hver farge. - Vi kan prøve med en rød og tre blå. Da er det bare to blå som er "to av samme farge":
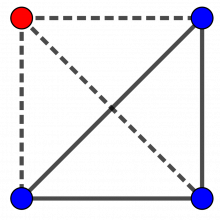
P(to av samme farge) = P(to blå) = \(\frac34\cdot\frac23=\frac{6}{12}=\frac12\). Hvis det er 1 rød og 3 blå brikker, får vi like mange forbindelser mellom brikker med like farger (heltrukken linje) som mellom brikker med ulike farger (stiplet linje).
Dette ble rettferdig.
Kan vi finne flere kombinasjoner som gir like store sannsynligheter for to like som for to ulike brikker?
Det går an hvis vi lar antall blå og røde brikker være to påfølgende trekanttall,
1 og 3, 3 og 6, 6 og 10, 10 og 15, osv.
Alle trekanttall er summen av heltall fra 1 og oppover, slik at trekanttall nr. n er \(\frac{1+n}2\cdot n=\frac{n(n+1)}{2}\), mens det påfølgende tallet er trekanttall nr. n + 1: \(\frac{n(1+n)}2 + (n+1)\).
Vi kaller det to tallene a og b, og totalt antall brikker er a + b. Vi lar CAS regne ut sannsynligheter:
Da må også sannsynligheten for å få en brikke av hver farge være \(\frac12\).
Vi kan vise at det er to påfølgende trekanttall som har denne egenskapen:
Vi tenker oss at vi har en mengde med a røde og b blå brikker, i alt a + b brikker.
Vi ønsker at sannsynligheten for å trekke to brikker av samme farge skal være \(\frac12\).
\(\begin{align} \frac{a}{a+b}\cdot \frac{a-1}{a+b-1}+\frac{b}{a+b}\cdot \frac{b-1}{a+b-1}&=\frac12\\ \frac{a^2-a+b^2-b}{a^2+ab-a+ab+b^2-b}&=\frac12\\ 2(a^2-a+b^2-b)&=a^2+ab-a+ab+b^2-b\\ 2a^2-2a+2b^2-2b-a^2-ab+a-ab-b^2+b&=0\\ a^2-2ab+b^2-a-b&=0\\ (a-b)^2&=a+b \end{align}\)
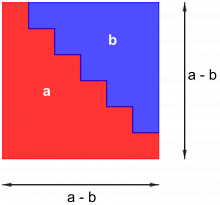
Det er nettopp to påfølgende trekanttall som oppfyller denne likningen:
Antall røde brikker + antall blå brikker, a + b, utgjør et like stort areal som kvadratet \((a-b)^2\).
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven viser flere måter å arbeide systematisk på for å løse et problem. Den kan brukes til å introdusere eller se tilbake på tabeller, valgtrær eller beregning av sannsynligheter. Det er neppe hensiktsmessig å introdusere alle metodene samtidig, men når elevene har fått litt forståelse av både kombinatorikk og sannsynlighet, kan en sammenligne ulike representasjoner og se sammenhengen mellom dem.
Mulig tilnærming
Fortell om Siri og Anna som har funnet en metode for å avgjøre hvem som skal ta oppvasken. La elevene arbeide i par med to røde og to blå brikker. Parene trekker to brikker hver gang og notere om resultatet blir Siri eller Anna. Ser det ut som de to jentene har funnet en rettferdig metode?
Samle resultatene fra alle parene på tavla, og legg sammen antall ganger hver av jentene må vaske opp. Med flere forsøk blir urettferdigheten tydeligere. Utfordre elevene til å finne en forklaring eller begrunnelse for at det ikke blir rettferdig. Her kan de komme med ulike argumenter og representasjoner, alt etter hva de har blitt kjent med tidligere. Hvis elevene følger teksten i oppgaven, vil de trekke to brikker samtidig. Kanskje trenger de en påminnelse om at når vi skal analysere en slik trekning, bør vi tenke oss at vi trekker én brikke om gangen. Vil det gjøre resultatet annerledes? Hvorfor ikke?
La elevene presentere ulike løsninger for hverandre. Dere må vurdere om alle løsningene er riktige. Hva er eventuelt feil? Hvor ligger misforståelsen?
Vurder om det er tid for å lansere en eller flere representasjoner i tillegg. Dere kan diskutere i fellesskap hvilke metoder dere finner mest effektive.
Neste problem er å finne en kombinasjon av røde og blå brikker som gir en rettferdig fordeling av oppvask. Lag en oversikt over kombinasjoner som kan prøves ut, og la hvert par prøve hver sin kombinasjon. Med fire brikker kan det være enten 2 + 2 eller 1 + 3. Bruk i tillegg kombinasjoner med fem, seks osv. brikker. Sørg for at noen kommer til å prøve ut kombinasjonen 1 + 3 og 3 + 6. Ved neste fellessamtale vil det være noen som har funnet rettferdige kombinasjoner. Hvilke kombinasjoner er det? Hva slags tall er det i disse kombinasjonene (trekanttall)? Hvis ingen elever ser det, kan du lansere teorien om at det blir rettferdig hvis antall røde og blå brikker er to påfølgende trekanttall. Så kan elevene teste ut flere kombinasjoner av to påfølgende trekanttall.
Gode veiledningsspørsmål
- Hvordan kan du avgjøre om trekningen blir rettferdig?
- Hvor mange forsøk tror du vi må gjøre før vi kan være sikre på at trekningen er rettferdig eller urettferdig?
- Er det noen måte å skrive eller tegne på som gir deg oversikt over de mulige resultatene i hver kombinasjon av røde og blå brikker?
- Kan du begrunne at det er riktig når du påstår at en trekning er enten rettferdig eller urettferdig?
Mulig utvidelse
Finn en generell begrunnelse for at det blir rettferdig med to påfølgende trekanttall – se løsningsforslaget.
Mulig støtte
La elevene få bruke brikker eller lignende slik at de virkelig kan trekke og prøve seg fram med konkreter.
Når elevene skal prøve ut ulike kombinasjoner, kan du sørge for at de som strever mest med forståelsen, ikke får så mange brikker å holde styr på.
Send inn elevsvar
Ressursen er utviklet av Matematikksenteret