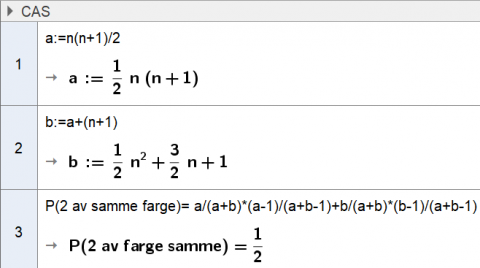Kven må ta oppvasken?
Aktivitet
To jenter, Siri og Anna, deler hybel. Dei er stadig uenige om kven som skal ta oppvasken, så dei vil løyse problemet ved trekking. Dei legg fire brikker i ei skål, to raude og to blå, og bestemmer seg for at dei skal trekkje to brikker. Dersom dei trekkjer to brikker med ulike fargar, skal Siri vaske opp, og dersom dei trekkjer to brikker med same farge, skal Anna vaske opp.
- Er dette ei rettferdig ordning? Vil dei måtte vaske opp omtrent like mange gonger kvar? Forklar korleis du har tenkt.
- Dersom det ikkje er rettferdig, kor mange brikker i kvar farge må dei leggje i skåla for at trekkinga skal bli rettferdig?
- Er det meir enn éin måte å kombinere raude og blå brikker på slik at trekkinga gir Siri og Anna omtrent like mange oppvaskar kvar?
Starthjelp
- Lag eit sett med brikker, og trekk fleire gonger, slik Siri og Anna gjorde.
- Prøv deg fram med å variere talet på raude og blå brikker.
- Kor mange forsøk meiner du det må gjerast før ein kan avgjere om ein kombinasjon av brikker er rettferdig?
- Har du ein måte å systematisere kombinasjonane av raude og blå brikker på?
- Kan du finne sannsynet for å trekkje to med same farge eller to med ulike fargar?
Løysing
Ordninga Siri og Anna kom fram til, var ikkje rettferdig. Vi kan vise det på fleire måtar. Legg merke til dei ulike måtane å forklare det på, og prøv å forstå alle.
1. Kombinatorikk, uordna utval:
Vi kan gi kvar brikke eit nummer og skrive opp alle moglege resultat av trekkingar:
| 1, 2 | 2, 3 |
| 1, 3 | 2, 4 |
| 1, 4 | 3, 4 |
To av seks utfall er brikker med same farge.
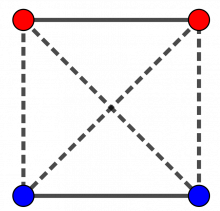
Vi kan også lage ei teikning av brikkene så vi er sikre på å få med alle moglege kombinasjonar. Vi let ei stipla linje binde saman to brikker av ulik farge, og trekkjer ei heil linje mellom to brikker med same farge. Resultatet blir det same:
Det går fire linjer mellom to brikker av ulik farge og to linjer mellom to av same farge. Det blir to utfall med to like fargar og fire utfall med to ulike fargar, så Siri kan rekne med å måtte ta dobbelt så mange oppvaskar som Anna.
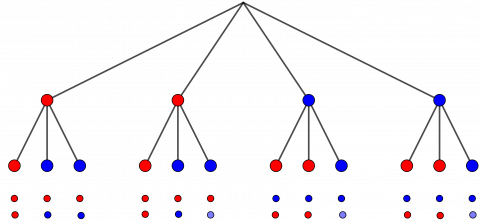
2. Kombinatorikk, ordna utval:
Vi kan teikne eit valtre eller lage ein tabell for å få oversikt over alle moglege kombinasjonar:
| R | R | B | B | |
| R | - | RR | RB | RB |
| R | RR | - | RB | RB |
| B | BR | BR | - | BB |
| B | BR | BR | BB | - |
Vi ser at det er 12 moglege utfall, og 4 av dei har to like fargar, medan 8 har to ulike fargar. Forholdet blir altså det same som i den førre løysinga: Siri må vaske opp dobbelt så mange gonger som Anna.
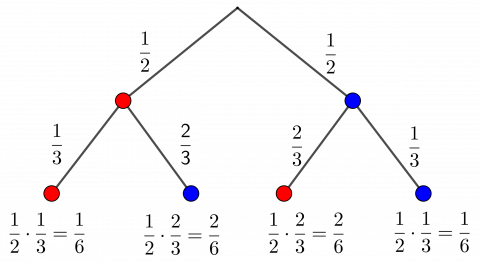
3. Sannsyn:
Vi kan teikne eit valtre eller setje opp ei utrekning med sannsyn for å vise det same som ovanfor:
\(\text{P(to av same farge) = P(raud og raud) + P(blå og blå)}\)
\(=\frac12\cdot\frac13+\frac12\cdot\frac13=\frac26=\frac13\)
\(\text{Da blir P(to av ulik farge) = 1 - P(to av same farge)}= 1-\frac13=\frac23\).
Vi prøver med andre mengder brikker i to fargar
- Vi kan prøve med to raude og fire blå brikker:
P(to av same farge) = P(to raude) + P(to blå)
\(=\frac26\cdot\frac15+\frac46\cdot\frac35=\frac2{30}+\frac{12}{30}=\frac{14}{30}=\frac7{15}\).
Dette er ikkje rettferdig, for sannsynet må bli \(\frac12\) for at det skal vere like sannsynleg å trekkje to like som to ulike. Men det var mykje nærare, så det var meir rettferdig enn med to brikker av kvar farge. - Vi kan prøve med ein raud og tre blå. Då er det berre to blå som er "to av same farge":
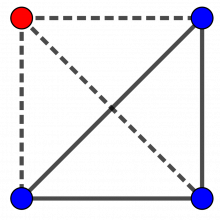
P(to av same farge) = P(to blå) = \(\frac34\cdot\frac23=\frac{6}{12}=\frac12\).Dersom det er 1 raud og 3 blå brikker, får vi like mange linjer mellom brikker med like fargar (heil linje) som mellom brikker med ulike fargar (stipla linje).
Dette vart rettferdig.
Kan vi finne fleire kombinasjonar som gir like stort sannsyn for to like som for to ulike brikker?
Det går an dersom vi let talet på blå og raude brikker vere to etterfølgjande trekanttal:
1 og 3, 3 og 6, 6 og 10, 10 og 15, osv.
Alle trekanttal er summen av heiltal frå 1 og oppover, slik at trekanttal nr. n er \(\frac{1+n}2\cdot n=\frac{n(n+1)}{2}\), mens det påfølgjande talet er trekanttal nr. n + 1: \(\frac{n(1+n)}2 + (n+1)\).
Vi kaller dei to tala a og b. Det totale talet på brikker er a + b. Vi let CAS regne ut sannsyn:
Då må også sannsynet for å få ei brikke av kvar farge vere \(\frac12\).
Vi kan vise at det er to etterfølgjande trekanttal som har denne eigenskapen:
Vi tenkjer oss at vi har ei mengde med a raude og b blå brikker, i alt a + b brikker.
Vi vil at sannsynet for å trekkje to brikker av same farge skal vere \(\frac12\).
\(\begin{align} \frac{a}{a+b}\cdot \frac{a-1}{a+b-1}+\frac{b}{a+b}\cdot \frac{b-1}{a+b-1}&=\frac12\\ \frac{a^2-a+b^2-b}{a^2+ab-a+ab+b^2-b}&=\frac12\\ 2(a^2-a+b^2-b)&=a^2+ab-a+ab+b^2-b\\ 2a^2-2a+2b^2-2b-a^2-ab+a-ab-b^2+b&=0\\ a^2-2ab+b^2-a-b&=0\\ (a-b)^2&=a+b \end{align}\)
Det er nettopp to etterfølgjande trekanttal som oppfyller denne likninga:
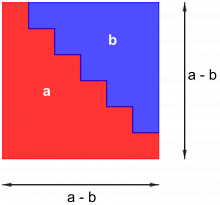
Talet på raude brikker + talet på blå brikker, a + b, utgjer eit like stort areal som kvadratet \((a-b)^2\).
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Oppgåva viser fleire måtar å arbeide systematisk på for å løyse eit problem. Ho kan brukast til å introdusere eller sjå tilbake på tabellar, valtre eller utrekningar av sannsyn. Det er nok ikkje tenleg å introdusere alle metodane samtidig, men når elevane har forstår litt av både kombinatorikk og sannsyn, kan ein samanlikne ulike representasjonar og sjå samanhengen mellom dei.
Mogleg tilnærming
Fortel om Siri og Anna som har funne ein metode for å avgjere kven som skal ta oppvasken. La elevane arbeide i par med to raude og to blå brikker. Para trekkjer to brikker kvar gong og noterer om resultatet blir Siri eller Anna. Ser det ut som dei to jentene har funne ein rettferdig metode?
Samle resultata frå alle para på tavla, og legg saman talet på gonger kvar av jentene må vaske opp. Med fleire forsøk blir urettferda tydelegare. Utfordre elevane til å finne ei forklaring eller grunngiving for at det ikkje blir rettferdig. Her kan dei kome med ulike argument og representasjonar, alt etter kva dei har fått kjennskap til tidlegare. Dersom elevane følgjer teksten i oppgåva, vil dei trekkje to brikker samtidig. Kanskje treng dei ei påminning om at når vi skal analysere ei slik trekking, bør vi tenkje oss at vi trekkjer éi brikke om gongen. Vil det gjere resultatet annleis? Kvifor ikkje?
La elevane presentere ulike løysingar for kvarandre. Dei må vurdere om alle løysingane er rette. Kva er eventuelt feil? Kvar ligg misforståinga?
Vurder om det er tid for å lansere ein eller fleire representasjonar i tillegg. De kan diskutere i fellesskap kva for metodar de meiner er mest effektive.
Neste problem er å finne ein kombinasjon av raude og blå brikker som gir ei rettferdig fordeling av oppvask. Lag ei oversikt over kombinasjonar som elevane kan prøve ut, og la kvart par prøve kvar sin kombinasjon. Med fire brikker kan det vere anten 2 + 2 eller 1 + 3. Bruk i tillegg kombinasjonar med fem, seks osv. brikker. Sørg for at nokre kjem til å prøve ut kombinasjonen 1 + 3 og 3 + 6. Ved neste fellessamtale vil det vere nokon som har funne rettferdige kombinasjonar. Kva kombinasjonar er det? Kva slags tal er det i desse kombinasjonane (trekanttal)? Dersom ingen elevar ser det, kan du lansere teorien om at det blir rettferdig dersom talet på raude og blå brikker er to etterfølgjande trekanttal. Så kan elevane teste ut fleire kombinasjonar av to etterfølgjande trekanttal.
Gode rettleiingsspørsmål
- Korleis kan du avgjere om trekkinga blir rettferdig?
- Kor mange forsøk trur du vi må gjere før vi kan vere sikre på at trekkinga er rettferdig eller urettferdig?
- Er det nokon måte å skrive eller teikne på som gir deg oversikt over dei moglege resultata i kvar kombinasjon av raude og blå brikker?
- Kan du grunngi at det er rett når du påstår at ei trekking er anten rettferdig eller urettferdig?
Mogleg utviding
Finn ei generell grunngiving for at det blir rettferdig med to etterfølgjande trekanttal – sjå forslaget til løysing.
Mogleg støtte
La elevane få bruke brikker eller liknande slik at dei kan trekkje og prøve seg fram med konkret.
Når elevane skal prøve ut ulike kombinasjonar, kan du sørgje for at dei som strevar mest med å forstå, ikkje får så mange brikker å halde styr på.
Send inn elevsvar
Ressursen er utviklet av Matematikksenteret