Legg sammen til 200
Aktivitet
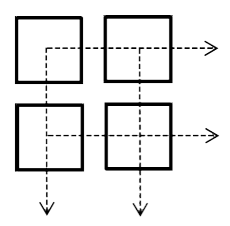
Velg fire siffer mellom 0 og 9, og plasser dem i hver sin rute i figuren nedenfor (du kan bruke samme siffer flere ganger):
- Les de to tosifrede tallene du får vannrett, og legg dem sammen.
- Les de to tosifrede tallene du får loddrett, og legg dem sammen.
- Legg til slutt sammen de to summene du har fått.
Eksempel:
Lag noen flere eksempler selv.
- Finnes det noen enkel måte for å avgjøre om summen blir et partall eller et oddetall?
- Kan du velge sifrene slik at summen av de fire tosifrede tallene blir 200?
Hvor mange måter kan du gjøre det på?
- Hvis vi bruker fire nuller, blir summen 0.
Hvis vi bruker fire niere, blir summen 396.
Hvilke tall mellom 0 og 396 er det mulig å lage?
Starthjelp
- Hvilke tall bidrar til sifferet du får på enerplassen?
- Hvilke tall bidrar til sifferet du får på tierplassen?
Løsning
1.
I de fire tallene vi legger sammen, er følgende siffer på enerplassen:
- sifferet øverst til høyre én gang
- sifferet nederst til venstre én gang
- sifferet nederst til høyre to ganger, og det betyr at disse to til sammen alltid blir et partall
Vi ser på mulige kombinasjoner av siffer på plassene øverst til høyre og nederst til venstre.
Hvis de to sifrene begge er partall eller begge er oddetall, blir de til sammen et partall, og da blir summen av de fire sifrene et partall:
Hvis de to tallene er et partall og et oddetall, blir summen av dem et oddetall, og da blir summen av de fire tallene et oddetall:
Det er altså sifrene øverst til høyre og nederst til venstre som avgjør om vi får et partall eller et oddetall til slutt.
2.
Det finnes mange løsninger på oppgaven.
Vi kan begynne med to tall som til sammen blir lik 100, og som er slik at sifrene på tierplassen til de to tallene blir lik 9. Eksempel: 45 + 55 = 100. Vi kan sette inn sifrene:
| 4 | 5 |
| 5 | 5 |
Summen av de to tallene når vi leser vannrett, er 45 + 55 = 100.
Summen av de to tallene når vi leser loddrett, er 45 + 55 = 100.
Til sammen blir det 200.
Merk: Samme siffer må stå øverst til høyre og nederst til venstre.
Kan du finne flere løsninger som er satt sammen på tilsvarende måte?
Vi kan bruke algebra for å løse problemet:
Vi lar a, b, c og d stå for de fire sifrene, og setter dem inn i de fire rutene:
| a | b |
| c | d |
Det første tallet som leses vannrett, må være 10a + b. Dette er det tosifrede tallet med a som første siffer og b som andre siffer.
Det andre tallet som leses vannrett, er 10c + d.
De to loddrette tallene er 10a + c og 10b + d.
Summen av disse fire tallene blir
10a + b + 10c + d + 10a + c + 10b + d
= 20a + 11b + 11c + 2d
=2(10a + d) + 11(b + c)
2(10a + d) vil alltid være et partall. Hvorfor?
11(b + c) blir et partall hvis b + c er et partall, og et oddetall hvis b + c er et oddetall. Hvorfor?
Merk: Her ser vi igjen at summen b + c avgjør om summen av alle de fire tallene blir et partall eller et oddetall.
Vi leter etter hvilke verdier av a, b, c og d som er slik at 2(10a + d) + 11(b + c) = 200.
Siden 200 er et partall, må b + c være et partall. Det betyr at b + c kan ha alle disse verdiene: 2, 4, 6, 8, 10, 12, 14, 16 og 18. Hvorfor kan ikke b + c være større enn 18?
10a + d er et tall mellom 0 og 99, så 2(10a + d) må være et tall mellom 0 og 198. Hvorfor?
Det blir svært mange mulige løsninger som gir 200 til sum.
3.
Det blir svært mange mulige løsninger. Det er enklere å finne ut hvilke summer vi ikke kan lage.
Hvis vi ser på uttrykket for summen som vi fant ovenfor, 2(10a + d) + 11(b + c), kan vi sette
x = 10a + d og y = b + c, for å vise at summen kan uttrykkes på formen 2x + 11y, der x kan være alle tall mellom 0 og 99, og y kan være alle tall mellom 1 og 18.
Vi ser at summen 2(10a + d) + 11(b + c) kan bli lik alle tall mellom 0 og 396, unntatt 1, 3, 5, 7 og 9.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven gir elevene anledning til å øve på addisjon i en mer interessant og utfordrende sammenheng enn vanlig. Det krever at de arbeider systematisk, noterer det de finner ut, og anvender forståelsen av plassverdisystemet.
Mulig tilnærming
Begynn med et 2 x 2-rutenett på tavla, og be elevene tegne det i boka.
Elevene velger selv fire siffer og fyller ut ett i hver rute. Be dem lese de to tosifrede tallene de får vannrett, og de to de får loddrett, og så legge dem sammen.
«Hva blir summen?»
Skriv opp alle summene som elevene har fått.
«Hva kan en matematiker spørre om nå?»
Hvis det ikke kommer noen forslag fra klassen, kan man foreslå:
- Hvilke svar kan man få?
- Hva er den minste mulige summen?
- Hva er den største mulige summen?
- Er det mulig å få alle tall mellom disse to tallene til svar?
- Kan vi få samme svar på mer enn én måte?
- Er det mulig å få 200 til sum?
- Når blir svarene partall, og når blir de oddetall?
La elevene få arbeide med de spørsmålene de ønsker, gjerne to og to.
Etter en stund kan man samle gruppene og la alle fortelle hva de har funnet ut. La det være åpent for spørsmål og diskusjon.
Noen kan ha vært opptatt av hva som virker inn på sifferet på enerplassen i den endelige summen, mens andre kan ha sett på hva som avgjør sifferet på tierplassen. I alle tilfeller er det viktig å få elevene til å forklare hva de har funnet ut. Vær spesielt oppmerksom på dem som finner gode måter å arbeide systematisk med undersøkelsene på, og la dem forklare hvordan de har tenkt og arbeidet.
Gode veiledningsspørsmål
- Hvordan vil de fire sifrene du velger, bidra til sifferet på enerplassen i den totale summen?
- Hvordan vil de fire sifrene du velger, bidra til sifferet på tierplassen i den totale summen?
Mulig utvidelse
- Hvert siffer kan brukes bare én gang.
- Det er ikke lov å bruke 0.
- Lag andre summer enn 200, for eksempel 100.
Ressursen er utviklet av NRICH