Legg saman til 200
Aktivitet
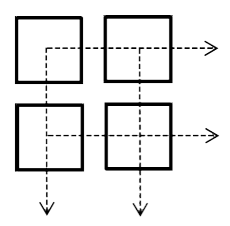
Vel fire siffer mellom 0 og 9, og plasser dei i kvar si rute i figuren nedanfor (du kan bruke same siffer fleire gonger):
-
Les dei to tosifra tala du får vassrett, og legg dei saman.
-
Les dei to tosifra tala du får loddrett, og legg dei saman.
-
Legg til slutt saman dei to summane du har fått.
Døme:
Lag nokre fleire døme sjølv.
1. Finnes det nokon enkel måte for å avgjere om summen blir eit partal eller eit oddetal?
2. Kan du velje siffera slik at summen av dei fire tosifra tala blir 200?
Kor mange måtar kan du gjere det på?
3. Viss vi bruker fire null, blir summen 0.
Viss vi bruker fire niarar, blir summen 396.
Kva tal mellom 0 og 396 er det mogleg å lage?
Starthjelp
- Kva tal bidreg til sifferet du får på einerplassen?
- Kva tal bidreg til sifferet du får på tiarplassen?
Løysing
1.
I dei fire tala vi legg saman, er følgjande siffer på einerplassen:
- sifferet øvst til høgre éin gong
- sifferet nedst til venstre éin gong
- sifferet nedst til høgre to gonger, og det betyr at desse to til saman alltid blir eit partal
Vi ser på moglege kombinasjonar av siffer på plassane øvst til høgre og nedst til venstre.
Viss dei to siffera begge er partal eller begge er oddetal, blir dei til saman eit partal, og då blir summen av dei fire siffera eit partal:
Viss dei to tala er eit partal og eit oddetal, blir summen av dei eit oddetal, og då blir summen av dei fire tala eit oddetal:
Det er altså siffera øvst til høgre og nedst til venstre som avgjer om vi får eit partal eller eit oddetal til slutt.
2.
Det finst mange løysingar på oppgåva.
Vi kan byrje med to tal som til saman blir lik 100, og som er slik at siffera på tiarplassen til dei to tala blir lik 9. Døme: 45 + 55 = 100. Vi kan setje inn siffera:
| 4 | 5 |
| 5 | 5 |
Summen av dei to tala når vi les vassrett, er 45 + 55 = 100.
Summen av dei to tala når vi les loddrett, er 45 + 55 = 100.
Til saman blir det 200.
Merk: Same siffer må stå øvst til høgre og nedst til venstre.
Kan du finne fleire løysingar som er sett saman på tilsvarande måte?
Vi kan bruke algebra for å løyse problemet:
Vi lèt a, b, c og d stå for dei fire siffera, og set dei inn i dei fire rutene:
| a | b |
| c | d |
Det første talet som blir lese vassrett, må vere 10a + b. Dette er det tosifra talet med a som første siffer og b som andre siffer.
Det andre talet som blir lese vassrett, er 10c + d.
Dei to loddrette tala er 10a + c og 10b + d.
Summen av desse fire tala blir
10a + b + 10c + d + 10a + c + 10b + d
= 20a + 11b + 11c + 2d
=2(10a + d) + 11(b + c)
2(10a + d) vil alltid vere eit partal. Kvifor?
11(b + c) blir eit partal viss b + c er eit partal, og eit oddetal viss b + c er eit oddetal. Kvifor?
Merk: Her ser vi igjen at summen b + c avgjer om summen av alle dei fire tala blir eit partal eller eit oddetal.
Vi leitar etter kva verdiar av a, b, c og d som er slik at 2(10a + d) + 11(b + c) = 200.
Sidan 200 er eit partal, må b + c vere eit partal. Det betyr at b + c kan ha alle desse verdiane: 2, 4, 6, 8, 10, 12, 14, 16 og 18. Kvifor kan ikkje b + c vere større enn 18?
10a + d er eit tal mellom 0 og 99, så 2(10a + d) må vere eit tal mellom 0 og 198. Kvifor?
Det blir svært mange moglege løysingar som gir 200 til sum.
3.
Det blir svært mange moglege løysingar. Det er enklare å finne ut kva summar vi ikkje kan lage.
Viss vi ser på uttrykket for summen som vi fann ovanfor, 2(10a + d) + 11(b + c), kan vi setje
x = 10a + d og y = b + c, for å vise at summen kan uttrykkjast på forma 2x + 11y, der x kan vere alle tal mellom 0 og 99, og y kan vere alle tal mellom 1 og 18.
Vi ser at summen 2(10a + d) + 11(b + c) kan bli lik alle tal mellom 0 og 396, bortsett frå 1, 3, 5, 7 og 9.
Lærarrettleiing
Kvifor arbeide med denne oppgåvan?
Denne oppgåva gir elevane høve til å øve på addisjon i ein meir interessant og utfordrande samanheng enn vanleg. Det krev at dei arbeider systematisk, noterer det dei finn ut, og nyttar forståinga av plassverdisystemet.
Mogleg tilnærming
Begynn med eit 2 x 2-rutenett på tavla, og be elevane teikne det i boka.
Elevane vel sjølv fire siffer og fyller ut eitt i kvar rute. Be dei lese dei to tosifra tala dei får vassrett, og dei to dei får loddrett, og så leggje dei saman.
«Kva blir summen?»
Skriv opp alle summane som elevane har fått.
«Kva kan ein matematikar spørje om no?»
Viss det ikkje kjem nokre forslag frå klassen, kan ein foreslå:
- Kva svar kan ein få?
- Kva er den minste moglege summen?
- Kva er den største moglege summen?
- Er det mogleg å få alle tal mellom desse to tala til svar?
- Kan vi få same svar på meir enn éin måte?
- Er det mogleg å få 200 til sum?
- Når blir svara partal, og når blir dei oddetal?
La elevane få arbeide med dei spørsmåla dei ønskjer, gjerne to og to.
Etter ei stund kan ein samle gruppene og la alle fortelje kva dei har funne ut. La det vere ope for spørsmål og diskusjon.
Nokon kan ha vore opptekne av kva som verkar inn på sifferet på einarplassen i den endelege summen, medan andre kan ha sett på kva som avgjer sifferet på tiarplassen. I alle tilfelle er det viktig å få elevane til å forklare kva dei har funne ut. Ver spesielt merksam på dei som finn gode måtar å arbeide systematisk med undersøkingane på, og la dei forklare korleis dei har tenkt og arbeid.
Gode rettleiingsspørsmål
- Korleis vil dei fire siffera du vel, bidra til sifferet på einarplassen i den totale summen?
- Korleis vil dei fire siffera du vel, bidra til sifferet på tiarplassen i den totale summen?
Mogleg utvidelse
- Kvart siffer kan brukast berre éin gong.
- Det er ikkje lov å bruke 0.
- Lag andre summar enn 200, til dømes 100
Ressursen er utviklet av NRICH