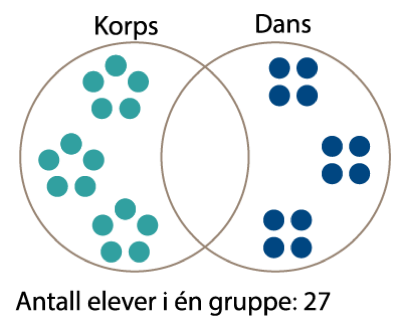Hobbyer i Karasjok
Problem
Ved en skole i Karasjok spiller 15 elever i korps, og 12 elever går på dans.
Hvor mange elever spiller både i korps og går på dans, dersom 13 elever gjør bare én av delene?
Løsning
Prøving og feiling med venndiagram
Det første venndiagrammet viser de 15 elevene som spiller i korps, og de 12 elevene som går på dans, som prikker. I dette diagrammet er alle plassert i bare én av gruppene:
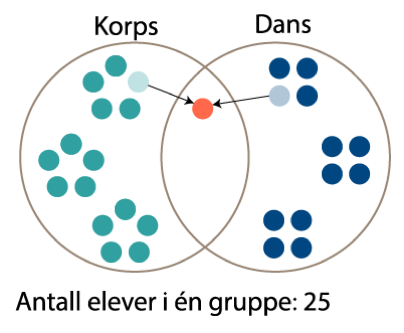
Når vi plasserer én elev i det overlappende området, må vi ta én fra hver gruppe, siden eleven som er i det overlappende området, er i begge gruppene. Det er fortsatt 15 elever i korpsgruppen og 12 i dansegruppen:
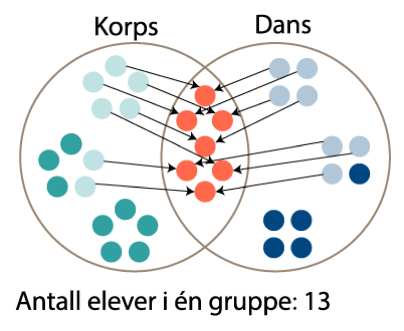
For hver elev som plasseres i det overlappende området, reduseres antall elever som er med i bare én av gruppene, med 2. Vi kan fortsette med å flytte elever over til det overlappende området helt til antall elever i bare én gruppe blir 13:
I det siste venndiagrammet ser vi at det er 13 elever som er med i bare én av gruppene, mens 7 elever er med på både korps og dans.
Algebra og venndiagram
15 elever spiller i korps, og 12 elever går på dans. Det vil si at det er 15 elever i den grønne sirkelen og 12 elever i den blå sirkelen.
De to sirklene kan overlappe hverandre slik at de danner et venndiagram:
Det fargelagte området (rosa + gul) inneholder \(13 + \textrm{gult område}\).
Ved å legge sammen den grønne sirkelen og den blå sirkelen vil vi få samme tall, bortsett fra at det overlappende området telles med to ganger. Det gir oss \(13+2\cdot \textrm{gult område}\) i stedet.
Det vil si at
\(\begin{align} 15+12&=13+2\cdot \textrm{gult område} \\ 14&=2\cdot \textrm{gult område} \\ \textrm{gult område}&=7 \end{align}\)
7 elever spiller både i korps og går på dans.
Vi kan også systematisere informasjonen i en tabell for å løse problemet.
Denne tabellen er fylt ut med hensyn til x, som tilsvarer antall elever i begge gruppene.
|
|
Dans |
|||
|
Korps |
|
Ja |
Nei |
Totalt |
|
Ja |
x |
15-x |
15 |
|
|
Nei |
12-x |
|
||
|
Totalt |
12 |
|
||
Vi vet at \(15-x\) og \(12-x\) til sammen blir 13, altså \(15-x+12-x=13\).
Deretter kan vi løse likningen:
\(\begin{align} 15-x+12-x&=13\\ 2x&=14\\ x&=7 \end{align}\)
Ressursen er utviklet av NRICH