LAST NED kopioriginaler

Andregradsfunksjoner I

Stikkord: Funksjonsuttrykk Grafer

Aktivitet

Du skal studere funksjonen \(g(x)=2x^2-8x+6\). Figuren nedenfor viser grafen til denne funksjonen.

Graf til funksjonen g(x)=2x^2-8x+6.

I tabellen nedenfor er det tre kolonner.

I den første kolonnen står de ulike bokstavene og tallene som er knyttet til funksjonsuttrykket og grafen.

I andre kolonne står navnene på disse tallene og bokstavene. Det er navn de har ut ifra den rollen de har i funksjonen.

I tredje kolonne står en forklaring til hver av navnene i kolonne to.

Én opplysning fra hver kolonne hører sammen.

1. Koble sammen en opplysning fra hver kolonne, slik at de tre opplysningene hører sammen.

g førstegradsleddet vi kan velge fritt hva denne bokstaven skal stå for
x nullpunkter inneholder ingen fri variabel
\(2x^2\) den frie variable der grafen skjærer x-aksen
\(-8x\) bunnpunkt inneholder den frie variable i andre grad
6 funksjonens navn der grafen skjærer y-aksen
2, -8 og 6 konstantleddet navnet på tallene som står sammen med de fri variable
(2, -2) der \(x=0\) vi bestemmer hva funksjonen skal hete
\(y=6\) koeffisienter inneholder den frie variable i første grad
\(x=1\) og \(x=3\) andregradsleddet punktet der grafen skifter retning fra synkende til stigende

Tabellen kan også skrives ut på et ark som du finner her. Du kan klippe ut alle rutene, da blir oppgaven å samle tre og tre som hører sammen.

Hint

  • Fri variabel. Vi kaller x i funksjonsuttrykket for fri variabel fordi vi fritt kan velge den verdien x skal ha.
  • Avhengig variabel. Vi kaller g for den avhengig variable, fordi g er en variabel som kan ha mange ulike verdier, men verdien er avhengig av hvilken verdi vi har valgt for x.
  • Leddene i funksjonen:
    • Andregradsleddet inneholder x og opphøyd i andre potens. Hvis funksjonen har andregradsledd, men ingen ledd med x opphøyd i en høyere potens, kalles funksjonen en andregradsfunksjon.
    • Førstegradsleddet er et ledd som inneholder x uten eksponent (fordi \(-8x=-8\cdot x^1\)).
    • Konstantleddet er et ledd som ikke inneholder noen x, der er bare et fast tall (her er x "usynlig" med, fordi \(6=6\cdot x^0\)).
  • Koeffisienter er navnet på tallene som står sammen med x. I funksjonen \(f(x)=ax^2+bx+c\) er a, b og c koeffisienter.
  • Bunnpunkt og toppunkt. Funksjonen kan ha bunnpunkt eller toppunkt. Dette er punktene som ligger høyest eller lavest på grafen innenfor et område. Når vi skal oppgi bunn- eller toppunkt til en funksjon, kan vi enten oppgi punktets koordinater eller punktets x-verdi.
  • Nullpunkter. Dette er punktene der funksjonsverdien er 0. På grafen er dette punkter der grafen skjærer x-aksen. Nullpunkter oppgis oftest bare med x-verdi, siden y-verdien alltid er 0.
  • Skjæringspunkt med y-aksen er punkter på grafen der \(x=0\). Punktet oppgis oftest bare med y-verdi. 

 

2. Tegn funksjonen \(\bf{g(x)=2x^2-8x+6}\) på papir.

  1. Fyll ut tabellen nedenfor, plott punktene inn i et koordinatsystem og tegn grafen så fint som mulig. Fikk du den til å bli like fin som GeoGebra sin graf?
    x -1 0 1 2 3 4 5
    y              

  2. Hva karakteriserer en parabel?

 

3. Flere tegneoppgaver

Tegn følgende grafer på papir:

  1. \(h(x)= x^2-5x+4\)
    Klarer du å plassere bunnpunktet riktig?
  2. \(k(x)=5-4x+x^2\)
    Har rekkefølgen på leddene i funksjonsuttrykket noe å si?
  3. \(s(x)=-x^2+2x+3\)
    Hvordan blir formen på grafen til denne funksjonen?

Starthjelp

  • Prøv først om du kan gjette hva begrepene står for.
  • Hvis du er usikker på hva faguttrykkene står for, kan du lese det som står under «Hint».

Til graftegning på papir:

  • Hvordan regner du ut verdien av andregradsleddet for de ulike x-verdiene?
  • Hvordan regner du ut funksjonsverdiene for negative x – verdier?
  • Hvordan regner du når koeffisienten er negativ?
  • Ser du noen symmetrier i punktene, enten i tabellen eller i det du har tegnet? Kan du bruke dette til å kontrollere om du har regnet og tegnet riktig?

Løsning

1. Koble sammen en opplysning fra hver kolonne, slik at de tre opplysningene hører sammen.

g funksjonens navn vi bestemmer hva funksjonen skal hete
x den frie variable vi kan velge fritt hva denne bokstaven skal stå for
\(2x^2\) andregradsleddet inneholder den frie variable i andre grad
\(-8x\) førstegradsleddet inneholder den frie variable i første grad
6 konstantleddet inneholder ingen fri variabel
2, -8 og 6 koeffisienter navnet på tallene som står sammen med den frie variable
(2, -2) bunnpunkt punktet der grafen skifter retning fra synkende til stigende
\(y=6\) der \(x=0\) inneholder den frie variable i første grad
\(x=1\) og \(x=3\) nullpunkter der grafen skjærer x-aksen

 

2. Tegn funksjonen \(\bf{g(x)=2x^2-8x+6}\) på papir.

  1. Tabellen du trenger for å tegne grafen til \(g(x)=2x^2-8x+6\):
    x -1 0 1 2 3 4 5
    y   6 0 -2 0 6  
    Legg merke til symmetrien i tabellen!
  2. En parabel har enten et toppunkt eller et bunnpunkt. Den er alltid symmetrisk om den loddrette linja gjennom topp eller bunnpunktet. Den har form som en U som åpner seg mer og mer.

3. Flere tegneoppgaver

  1. Bunnpunktet ligger midt mellom \(x=2\) og \(x=3\), lag et punkt i tabellen for \(x=2,5\). Bunnpunktet ligger i (2,5, -2,25).
    Grafen til h(x)=x^2-5x+4
  2. Rekkefølgen av leddene har ikke noe å si. Men funksjonen må ha et andregradsledd for at grafen skal bli en parabel. Dette er et eksempel på en parabel som ikke har noen nullpunkter.
    Grafen til k(x)=5-4x+x^2
  3. Også denne grafen er en parabel, men den har toppunkt i stedet for bunnpunkt.
    Grafen til s(x)=-x^2+2x+3

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

Når vi arbeider med andregradsfunksjoner, bruker vi mange faguttrykk som er nye for elevene. Tanken med denne aktiviteten er å gjøre elevene kjent med de fleste begrepene idet de starter å arbeide med andregradsfunksjoner. Dette innebærer også å se på noen sammenhenger mellom graf og funksjonsuttrykk.

Mulig tilnærming

Du kan vurdere hva som passer best for dine elever: Kanskje må du fortelle litt om de nye begrepene før de får begynne å arbeide på egen hånd, eller så kan de få den første oppgaven uten videre forklaring først.

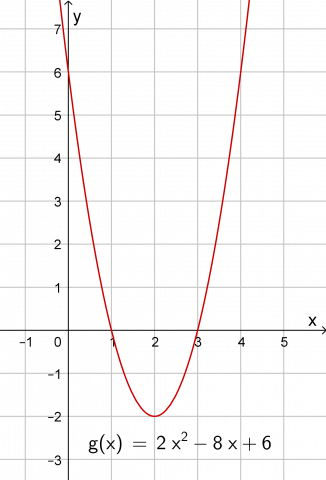
Oppgaven fins på en kopioriginal her. Du kan skrive dem ut på forhånd og klippe opp rutene og legge settene fra hver kopioriginal i hver sin konvolutt. Tallene og begrepene som er brukt, er knyttet til funksjonen \(g(x)=2x^2-8x+6\) og grafen til denne funksjonen. De må få se funksjonsuttrykket og grafen hele tiden mens de arbeider, enten på tavla eller at de tegner grafen hver for seg i GeoGebra.

La elevene arbeide i par. Fortell elevene at i konvolutten ligger flere brikker som skal ordnes i tripler som hører sammen. Det er brukt tre ulike farger, og det skal være en av hver farge i hvert trippel. Alternativt kan hvert par få et ark med beskjed om at de skal forbinde med streker det som hører sammen, en rute i hver kolonne hører sammen.

Følg med mens elevene arbeider. Kanskje vil du se at de intuitivt ser hva som hører sammen eller at de kjenner en del begreper fra før. Kanskje får du et inntrykk av hvilke begreper som oppleves som vanskelige. Når de fleste er ferdige, er det tid for en felles samtale hvor forslag diskuteres og alt settes på plass. Er det noe som er uklart? Vanskelig? Dukker det opp flere spørsmål i løpet av arbeidet er det fint å få også det avklart.

I det videre arbeidet med andregradsfunksjoner, bruker vi disse begrepene bevisst slik at de fort kan feste seg og bli en del av det felles fagspråket.

Det neste punktet er at elevene selv skal tegne grafen på papir. De kommer antakelig sjelden til å tegne grafer på papir, men litt erfaring må de få. Det første er å tegne grafen de allerede har arbeidet med. Her kan utfordringen kanskje være å fylle ut tallene i tabellen, særlig å regne ut y-verdiene der x er negative tall. Ta dere tid til å diskutere og avklare dette.

Du må også følge med på tegneprosessen. Det er ikke lov å bruke linjal. Og grafen skal ha en fin bue der den snur, - den skal ikke være spiss. Oppsummer i felleskap hvilke egenskaper som karakteriserer parabler.

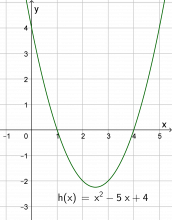
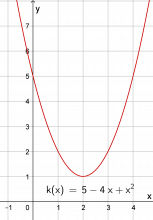
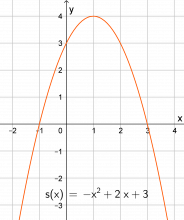
Oppgave 3 har tre nye funksjoner som elevene skal tegne grafer til på papir. Kanskje kan dette være en ekstra øving, kanskje en lekse. Men spørsmålene som følger oppgavene, må diskuteres og avklares i hele klassen.

Til slutt kan det være en ide å la elevene skrive en læringslogg hvor de samler alle nye begreper og knytter dem til funksjonsuttrykket eller til grafen.

Gode veiledningsspørsmål

  • Må en andregradsfunksjon inneholde både andregradsledd, førstegradsledd og konstantledd?
  • Hvilke ledd må funksjonsuttrykket inneholde?
  • Hvordan regner man ut andregradsleddet i funksjonen når man fyller ut tabeller?
  • Hvordan regner du ut funksjonsverdiene for negative x-verdier?
  • Hvordan regner man ut andregradsleddet når koeffisienten er negativ?
  • Ser du noen symmetrier i punktene, enten i tabellen eller i det du har tegnet? Kan du bruke dette til å kontrollere at du har regnet og tegnet riktig?

Mulig utvidelse

Denne aktiviteten er den første i en serie om andregradsfunksjoner:

Ressursen er utviklet av Matematikksenteret

Denne ressursen er lisensiert under Navngivelse-IkkeKommersiell CC BY-NC CC BY-NC
9,10