LAST NED kopioriginaler

Andregradsfunksjonar I

Stikkord: Funksjonsuttrykk Grafer

Aktivitet

Du skal studere funksjonen \(g(x)=2x^2-8x+6\). Figuren nedanfor viser grafen til denne funksjonen.

Graf til funksjonen g(x)=2x^2-8x+6.

I tabellen nedanfor er det tre kolonnar.

I den første kolonnen står bokstavane og tala som er knytte til funksjonsuttrykket og grafen.

I den andre kolonnen står namna på desse tala og bokstavane. Det er namn dei har ut frå den rolla dei har i funksjonen.

I den tredje kolonnen står det ei forklaring til kvart av namna i kolonne 2.

1. Kople saman éi opplysning frå kvar kolonne, slik at dei tre opplysningane høyrer saman.

g førstegradsleddet Vi kan velje fritt kva denne bokstaven skal stå for
x nullpunkt inneheld ingen fri variabel
\(2x^2\) den frie variabelen der grafen skjer x-aksen
\(-8x\) botnpunkt inneheld den frie variabelen i andre grad
6 namnet på funksjonen der grafen skjer y-aksen
2, -8 og 6 konstantleddet namnet på tala som står saman med dei frie variablane
(2, -2) der \(x=0\) vi bestemmer kva funksjonen skal heite
\(y=6\) koeffisientar inneheld den frie variabelen i første grad
\(x=1\) og \(x=3\) andregradsleddet punktet der grafen skifter retning frå fallande til stigande

Tabellen kan også skrivast ut på eit ark som du finn her. Du kan klippe ut alle rutene, og då blir oppgåva å samle tre og tre som høyrer saman.

Hint

  • Fri variabel. Vi kallar x i funksjonsuttrykket for fri variabel fordi vi fritt kan velje den verdien x skal ha.
  • Avhengig variabel. Vi kallar g for avhengig variabel, fordi g kan ha mange ulike verdiar, men verdien er avhengig av kva verdi vi har valt for x.
  • Ledda i funksjonen:
    • Andregradsleddet inneheld x og opphøgd i andre potens. Dersom funksjonen har andregradsledd, men ingen ledd med x opphøgd i ein høgare potens, kallar vi funksjonen andregradsfunksjon.
    • Førstegradsleddet er eit ledd som inneheld x utan eksponent (fordi \(-8x=-8\cdot x^1\)).
    • Konstantleddet er eit ledd som ikkje inneheld nokon x. Det har berre eit fast tal (her er x "usynleg" med, fordi \(6=6\cdot x^0\)).
  • Koeffisientar er namnet på tala som står saman med x. I funksjonen \(f(x)=ax^2+bx+c\) er a, b og c koeffisientar.
  • Botnpunkt og toppunkt. Funksjonen kan ha botnpunkt eller toppunkt. Det er punkta som ligg høgast eller lågast på grafen innanfor eit område. Når vi skal oppgi botn- eller toppunkt til ein funksjon, kan vi anten oppgje koordinatane til punktet eller x-verdien til punktet.
  • Nullpunkt er punkt der funksjonsverdien er 0. På grafen er dette punkt der grafen skjer x-aksen. Nullpunkt blir oftast oppgitte berre med x-verdien, sidan y-verdien alltid er 0.
  • Skjæringspunkt med y-aksen er punkt på grafen der x = 0. Punktet blir oftast oppgitt berre med y-verdien.

 

2. Teikn funksjonen \(\bf{g(x)=2x^2-8x+6}\) på papir.

  1. Fyll ut tabellen nedanfor, plott punkta inn i eit koordinatsystem, og teikn grafen så fint du kan. Fekk du han til å bli like fin som grafen i GeoGebra?
    x -1 0 1 2 3 4 5
    y              

  2. Kva karakteriserer ein parabel?

 

3. Fleire teikneoppgåver

Teikn desse grafane på papir:

  1. \(h(x)= x^2-5x+4\)
    Klarer du å plassere botnpunktet rett?
  2. \(k(x)=5-4x+x^2\)
    Har rekkjefølgja på ledda i funksjonsuttrykket noko å seie?
  3. \(s(x)=-x^2+2x+3\)
    Korleis blir forma på grafen til denne funksjonen?

Starthjelp

  • Prøv først om du kan gjette kva omgrepa står for.
  • Dersom du er usikker på kva faguttrykke står for, kan du lese det som står under "Hint".

Til grafteikning på papir:

  • Korleis reknar du ut verdien av andregradsleddet for dei ulike x-verdiane?
  • Korleis reknar du ut funksjonsverdiane for negative x-verdiar?
  • Korleis reknar du når koeffisienten er negativ?
  • Ser du nokre symmetriar i punkta, anten i tabellen eller i det du har teikna? Kan du bruke det til å kontrollere om du har rekna og teikna rett?

Løysing

1. Koble sammen en opplysning fra hver kolonne, slik at de tre opplysningene hører sammen.

g namnet på funksjonen vi bestemmer kva funksjonen skal heite
x den frie variabelen vi kan velje fritt kva denne bokstaven skal stå for
\(2x^2\) andregradsleddet inneheld den frie variabelen i andre grad
\(-8x\) førstegradsleddet inneheld den frie variabelen i første grad
6 konstantleddet inneheld ingen fri variabel
2, -8 og 6 koeffisientar namnet på tala som står saman med dei frie variablane
(2, -2) botn punktet der grafen skifter retning frå fallande til stigande
\(y=6\) der \(x=0\) der grafen skjer y-aksen
\(x=1\) og \(x=3\) nullpunkt der grafen skjer x-aksen

 

2. Teikn funksjonen \(\bf{g(x)=2x^2-8x+6}\) på papir.

  1. Tabellen du treng for å teikne grafen til \(g(x)=2x^2-8x+6\):
    x -1 0 1 2 3 4 5
    y   6 0 -2 0 6  
    Legg merke til symmetrien i tabellen!
  2. En parabel har anten eit toppunkt eller eit botnpunkt. Han er alltid symmetrisk om den loddrette linja gjennom topp- eller botnpunktet. Han har form som en U som åpner seg mer og mer.

3. Fleire teikneoppgåver

  1. Botnpunktet ligg midt mellom \(x=2\) og \(x=3\). Lag eit punkt i tabellen for \(x=2,5\). Botnpunktet ligg i (2,5, -2,25).
    Grafen til h(x)=x^2-5x+4
  2. Rekkjefølgja av ledda har ikkje noko å seie. Men funksjonen må ha eit andregradsledd for at grafen skal bli ein parabel. Dette er eit eksempel på ein parabel som ikkje har noko nullpunkt.
    Grafen til k(x)=5-4x+x^2
  3. Også denne grafen er ein parabel, men han har toppunkt i staden for botnpunkt.
    Grafen til s(x)=-x^2+2x+3

Lærarrettleiing

Kvifor arbeide med denne oppgåva?

Når vi arbeider med andregradsfunksjonar, bruker vi mange faguttrykk som er nye for elevane. Tanken med denne aktiviteten er at elevane skal få kjennskap til dei fleste omgrepa når dei begynner å arbeide med andregradsfunksjonar. Det inneber også å sjå på nokre samanhengar mellom graf og funksjonsuttrykk.

Mogleg tilnærming

Du kan vurdere kva som passar best for dine elevar. Kanskje må du fortelje litt om dei nye omgrepa før dei får begynne å arbeide på eiga hand, eller så kan dei få den første oppgåva utan vidare forklaring først.

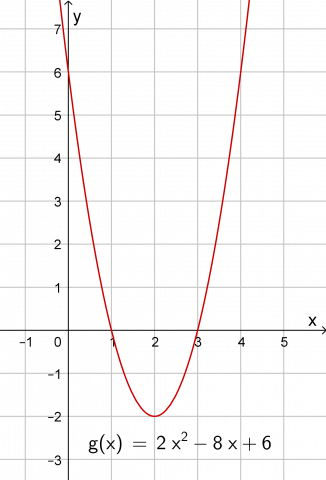
Oppgaven fins på en kopioriginal her. Du kan skrive dei ut i førevegen, klippe opp rutene og leggje setta frå kvar kopioriginal i kvar sin konvolutt. Tala og omgrepa som er nytta, er knytte til funksjonen \(g(x)=2x^2-8x+6\)

og grafen til denne funksjonen. Elevane må få sjå funksjonsuttrykket og grafen heile tida medan dei arbeider, anten på tavla eller ved at dei teiknar grafen kvar for seg i GeoGebra.

La elevane arbeide i par. Fortel dei at i konvolutten ligg det fleire brikker som skal ordnast i triplar som høyrer saman. Det er brukt tre ulike fargar, og det skal vere ein av kvar farge i kvar trippel. Alternativt kan kvart par få eit ark der dei skal forbinde med strekar ei rute i kvar kolonne som høyrer saman.

Følg med medan elevane arbeider. Kanskje vil du oppdage at dei intuitivt ser kva som høyrer saman, eller at dei kjenner ein del omgrep frå før. Kanskje får du eit inntrykk av kva for omgrep dei synest er vanskelege. Når dei fleste er ferdige, er det tid for ein felles samtale der de diskuterer og set alt på plass. Er det noko som er uklart eller vanskeleg? Dukkar det opp fleire spørsmål under arbeidet, er det bra å få avklart det også.

I arbeidet vidare med andregradsfunksjonar bruker vi desse omgrepa bevisst slik at dei fort kan feste seg og bli ein del av det felles fagspråket.

Det neste punktet er at elevane sjølve skal teikne grafen på papir. Dei kjem truleg sjeldan til å teikne grafar på papir, men litt erfaring må dei få. Det første er å teikne grafen dei alt har arbeidd med. Her kan utfordringa kanskje vere å fylle ut tala i tabellen, særleg å rekne ut y-verdiane der x er negative tal. Bruk tid på å diskutere og avklare dette.

Du må også følgje med på teikneprosessen. Det er ikkje lov å bruke linjal. Og grafen skal ha ein fin boge der han snur – han skal ikkje vere spiss. Summer opp i fellesskap dei eigenskapane som karakteriserer parablar.

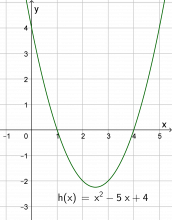
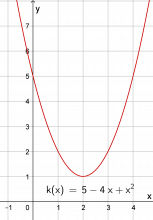
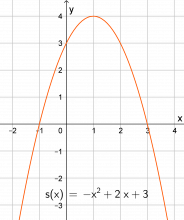
Oppgåve 3 har tre nye funksjonar som elevane skal teikne grafar til på papir. Kanskje kan det vere ei ekstra øving, kanskje ei lekse. Men spørsmåla som følgjer oppgåvene, må diskuterast og avklarast i heile klassen.

Til slutt kan det vere ein idé å la elevane skrive ein læringslogg der dei samlar alle nye omgrep og knyter dei til funksjonsuttrykket eller til grafen.

Gode rettleiingsspørsmål

  • Må ein andregradsfunksjon innehalde både andregradsledd, førstegradsledd og konstantledd?
  • Kva ledd må funksjonsuttrykket innehalde?
  • Korleis reknar du ut andregradsleddet i funksjonar når du fyller ut tabellar?
  • Korleis reknar du ut funksjonsverdiane for negative x-verdiar?
  • Korleis reknar du ut andregradsleddet når koeffisienten er negativ?
  • Ser du nokre symmetriar i punkta, anten i tabellen eller i det du har teikna? Kan du bruke det til å kontrollere at du har rekna og teikna rett?

Mogleg utviding

Denne aktiviteten er den første i ein serie om andregradsfunksjonar:

Ressursen er utviklet av Matematikksenteret

Denne ressursen er lisensiert under Navngivelse-IkkeKommersiell CC BY-NC CC BY-NC
9,10