Tårnet har mange sider
Aktivitet
Til denne aktiviteten trenger du terninger eller centikuber.
Du skal bygge et tårn ved å sette terninger oppå hverandre. Tell antall synlige sider på alle terningene i tårnet. Bygg tårn med ulike høyder.
1. Hva er sammenhengen mellom antall terninger og antall synlige sider?
Beskriv sammenhengen med ord.
Kan du lage en oversikt over antall synlige sider med tårn på 1, 2, 3, 4 og 5 terninger? Hvor mange synlige sider tror du det ville være om du hadde klart å lage et tårn med 100 terninger?
La antall terninger være n. Kan du beskrive sammenhengen mellom antall terninger og antall synlige sider med et algebrauttrykk?
2. Hva er sammenhengen mellom antall terninger og antall sider som ikke er synlige?
Kan du beskrive denne sammenhengen både med ord og med et algebraisk uttrykk?
3. Ekstra utfordring:
Kan du tegne en graf som viser hvordan antall synlige sider øker når antall terninger øker?
Og en annen graf som viser sammenhengen mellom antall terninger og antall usynlige sider?
Starthjelp
Til spørsmål 1:
- Hvor mange sider er synlige når «tårnet» består av bare én terning?
- Hvor mange sider er synlige når vi bruker to terninger?
- Hvor mange flere synlige sider blir det for hver ny terning?
Til spørsmål 2:
- Hvor mange sider er usynlige når «tårnet» består av bare én terning?
- Hvor mange sider er usynlige når vi bruker to terninger?
- Hvor mange flere usynlige sider blir det for hver ny terning?
Løsning
Det er mange måter å forklare hvordan man regner ut antall sider. Vi har valgt et eksempel nedenfor, men hvis du har en annen forklaring, kan du bruke den.
Vi kan lage en tabell som viser sammenhengen:
1. Hva er sammenhengen mellom antall terninger og antall synlige sider?
|
Antall terninger |
Antall synlige sider |
Forklaring |
|
\(1\) |
\(5\) |
Med ord:
|
|
\(2\) |
\(9 = 2 \cdot4 + 1\) |
|
|
\(3\) |
\(13 = 3 \cdot4 + 1\) |
|
|
\(4\) |
\(17 = 4 \cdot 4 + 1\) |
|
|
… |
|
|
|
\(100\) |
\(401=100 \cdot 4 + 1\) |
|
|
… |
|
|
|
\(n\) |
\(n \cdot 4 + 1\) |
Algebrauttrykk som beskriver antall synlige sider |
2. Hva er sammenhengen mellom antall terninger og antall sider som ikke er synlige?
|
Antall terninger |
Antall usynlige sider |
Forklaring |
|
\(1\) |
\(1\) |
Med ord:
|
|
\(2\) |
\(3 = 2 + 1\) |
|
|
\(3\) |
\(5 = 2\cdot2 + 1\) |
|
|
\(4\) |
\(7 = 2 \cdot3 + 1\) |
|
|
… |
|
|
|
\(100\) |
\(199=99 \cdot 2 + 1\) |
|
|
… |
|
|
|
\(n\) |
\((n-1)\cdot 2 + 1=2n-1\) |
Algebrauttrykk som beskriver antall usynlige sider |
Hvis vi summerer antall synlige og usynlige sider får vi 6 ganger antall terninger. Hvorfor?
Kontroll med 100 terninger: \(401+199=600=100 \cdot 6\)
3. Ekstra utfordring, antall synlige sider
Vi kan betrakte antall terninger som den frie variable x og antall synlige sider som den avhengig variable y i et uttrykk som beskriver sammenhengen mellom dem:
\(y = (x-1)\cdot 4 + 5\)
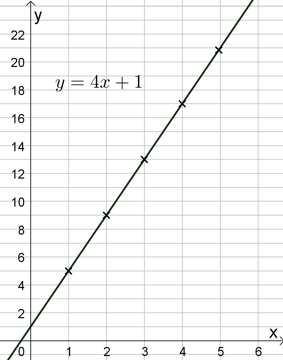
Vi kan tegne en graf som viser denne sammenhengen. Grafen hjelper oss med å finne antall synlige sider for alle mulige antall terninger. Men vi må være oppmerksomme på at denne grafen bare er gyldig for hele, positive tall på x-aksen, dvs. for 1, 2, 3 osv. terninger. Punktene er merket med x på grafen.
Hvis vi regner ut og forenkler funksjonsuttrykket får vi \(y = 4x + 1\). Vi tegner grafen til denne funksjonen.
\(y = (x-1)\cdot 4 + 5 \\ y=4x-4+5\\ y=4x+1\)
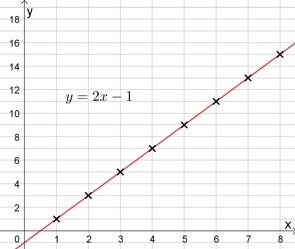
Antall usynlige sider kan vises med følgende graf. Den er også gyldig bare for hele, positive verdier av x.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Gjennom denne aktiviteten blir elevene utfordret til å lete etter mønster og beskrive dette på flere måter, - med ord, med et systematisk oppsett, med algebraisk uttrykk og eventuelt med graf. De må gå fra å finne et mønster gjennom systematiske undersøkelser til å generalisere resultatene.
Mulig tilnærming
La elevene arbeide i par, og sørg for at alle parene har minst fem like store kuber (centikuber eller terninger).
Be dem legge en terning på bordet og spør hvor mange sider som er synlige. Det er enkelt å bli enige om at det er fem sider. Be dem så sette to terninger oppå hverandre. Hvor mange sider er synlige nå? Herfra kan hvert par arbeide med sine terninger.
Oppgaven er å finne fram til mønsteret i hvordan antall synlige sider vokser for hver ny terning som legges på og å beskrive dette mønsteret med ord. Utfordre elevene til å prøve å skrive dette ned på en oversiktlig måte.
Følg med på arbeidet og samtalene i arbeidsparene. Når du stopper arbeidet for å oppsummere i fellesskap, kan flere par fortelle hvordan de beskriver sammenhengen med ord. Skriv alle forklaringene ned på tavla. For eksempel:
En elev forklarer: «Jeg ser fire sider på alle treningene pluss en ekstra side på toppen.»
En annen elev forklarer: «Jeg ser fem sider på den øverste terningen og fire på alle de andre.»
Det kan komme flere forslag, alle må noteres.
Be elevene regne ut antall synlige sider for 5, 10 og 100 terninger med hver av forklaringene som utgangspunkt. Ga alle forklaringene samme svar?
Sett opp regnestykkene på tavla:
|
Antall terninger |
Fire sider på alle terningene pluss en ekstra side på toppen |
Fem sider på den øverste terningen og fire på alle de andre
|
Evt. andre forklaringer |
|
\(5\) |
\(5 \cdot 4 + 1 = 21\) |
\(5 + 4 \cdot 4 = 21\) |
… |
|
\(10\) |
\(10 \cdot 4 + 1 =41\) |
\(5 + 4 \cdot 9 = 41\) |
… |
|
\(100\) |
\(100 \cdot 4 + 1 =401\) |
\(5 + 4 \cdot 99 = 401\) |
… |
|
|
|
|
|
Hvis forklaringene er riktige, vil de gi samme svar. Be elevene se på en og en forklaringsmodell om gangen og finne ut hva som er fast og hva som forandres for hvert nytt regnestykke. Hva hvis antall terninger var ukjent? Hva hvis vi sier at vi har n terninger, hvordan ville utregningene ha sett ut da? Få elevene med på at vi kunne ha føyd til en siste linje i tabellen:
|
\(n\) |
\(n \cdot 4 + 1 \) |
\(5 + 4 \cdot (n-1) \) |
… |
Disse uttrykkene er generelle formler som kan brukes uansett hvor mange terninger vi har i tårnet. Det gjenstår å vise at de er like. La elevene undersøke om alle formlene kan forenkles slik at de blir like.
De ender sikkert opp med formelen \(4n + 1\). Et par spørsmål til må avklares:
- Kan man fortsatt bruke en av de andre formlene, f.eks. \(5 + 4(n – 1)\)?
- Vi sier at en formel med en bokstav som kan stå for mange ulike tall, er en generell formel. Hva er fordelene med å finne generelle formler?
I aktiviteten er det tatt med et ekstra spørsmål om å tegne en graf som forteller sammenhengen mellom antall terninger og antall synlige sider. Du må vurdere om dette passer inn i arbeidet på dette tidspunktet. Hvis du vil vise hvor mange ulike representasjoner som kan beskrive samme sammenheng, er det fint å også trekke inn grafen. Men da må dere samtidig ta opp at selv om denne grafen tegnes som en sammenhengende linje, er den gyldig bare i de punktene der x-verdien er et positivt heltall, siden den angir antall terninger i tårnet.
Oppgaven med å gjøre tilsvarende undersøkelser med antall usynlige sider, blir en gjentakelse, - en øvelse i å gjøre det samme med utgangspunkt i en litt annerledes situasjon.
Gode veiledningsspørsmål
- Hvordan teller du for å finne antall synlige sider når du har 2 terninger, 3 terninger, 4 terninger?
- Kan du forklare hvordan man bør telle systematisk hver gang?
- Kan du skrive ned hvordan du har regnet ut antall synlige sider i hvert av tilfellene?
Mulig utvidelse
Kanskje er det å tegne grafer en utvidelse av oppgaven som ikke alle elevene skal være med på?
Kanskje vil noen diskutere hvordan man skal tolke verdien der grafen skjærer y-aksen, altså «antall synlige sider er 1 hvis vi har 0 terninger»? Kan dette gi mening?
Elevene kan oppfordres til å lage andre varianter av oppgaven, for eksempel tårn med to og to terninger inntil hverandre, eller andre figurer som vokser etter et gitt mønster. Så kan de finne regler og formler for hvordan antall synlige sider øker når antall terninger øker.
Ressursen er utviklet av Matematikksenteret