Tårnet har mange sider
Aktivitet
Til denne aktiviteten treng du terningar eller centikubar.
Du skal byggje eit tårn ved å setje terningar oppå kvarandre. Tell talet på synlege sider på alle terningane i tårnet. Bygg tårn med ulike høgder.
1. Kva er samanhengen mellom talet på terningar og talet på synlege sider?
Beskriv samanhengen med ord.
Kan du lage ei oversikt over talet på synlege sider med tårn på 1, 2, 3, 4 og 5 terningar? Kor mange synlege sider trur du det ville vere om du hadde klart å lage eit tårn med 100 terningar?
La talet på terningar vere n. Kan du beskrive samanhengen mellom talet på terningar og talet på synlege sider med eit algebrauttrykk?
2. Kva er samanhengen mellom talet på terningar og talet på sider som ikkje er synlege?
Kan du beskrive denne samanhengen både med ord og med eit algebraisk uttrykk?
3. Ekstra utfordring:
Kan du teikne ein graf som viser korleis talet på synlege sider aukar når talet på terningar aukar?
Og ein annan graf som viser samanhengen mellom talet på terningar og talet på usynlege sider?
Starthjelp
Til spørsmål 1:
-
Kor mange sider er synlege når «tårnet» består av berre éin terning?
-
Kor mange sider er synlege når vi bruker to terningar?
-
Kor mange fleire synlege sider blir det for kvar ny terning?
Til spørsmål 2:
-
Kor mange sider er usynlege når «tårnet» består av berre éin terning?
-
Kor mange sider er usynlege når vi bruker to terningar?
-
Kor mange fleire usynlege sider blir det for kvar ny terning?
Løysing
Det er mange måtar å forklare korleis ein reknar ut talet på sider. Vi har valt eit døme nedanfor, men viss du har ei anna forklaring, kan du bruke ho.
Vi kan lage ein tabell som viser samanhengen:
1. Kva er samanhengen mellom talet på terningar og talet på synlege sider?
|
Tal på terningar |
Tal på synlege sider |
Forklaring |
|
\(1\) |
\(5\) |
Med ord:
|
|
\(2\) |
\(9 = 2 \cdot4 + 1\) |
|
|
\(3\) |
\(13 = 3 \cdot4 + 1\) |
|
|
\(4\) |
\(17 = 4 \cdot 4 + 1\) |
|
|
… |
|
|
|
\(100\) |
\(401=100 \cdot 4 + 1\) |
|
|
… |
|
|
|
\(n\) |
\(n \cdot 4 + 1\) |
Algebrauttrykk som beskriv talet på synlege sider |
2. Kva er samanhengen mellom talet på terningar og talet på sider som ikkje er synlege?
|
Tal på terningar |
Tal på usynlege sider |
Forklaring |
|
\(1\) |
\(1\) |
Med ord:
|
|
\(2\) |
\(3 = 2 + 1\) |
|
|
\(3\) |
\(5 = 2\cdot2 + 1\) |
|
|
\(4\) |
\(7 = 2 \cdot3 + 1\) |
|
|
… |
|
|
|
\(100\) |
\(199=99 \cdot 2 + 1\) |
|
|
… |
|
|
|
\(n\) |
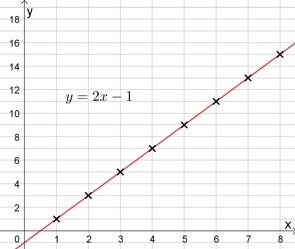
\((n-1)\cdot 2 + 1=2n-1\) |
Algebrauttrykk som beskriv talet på usynlege sider |
Viss vi summerer talet på synlege og usynlege sider får vi 6 gonger talet på terningar. Kvifor?
Kontroll med 100 terningar: \(401+199=600=100 \cdot 6\)
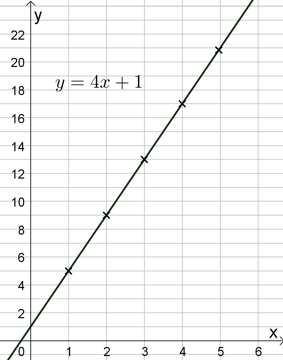
3. Ekstra utfordring, tal på synlege sider
Vi kan vurdere talet på terningar som den frie variable x-en og talet på synlege sider som den avhengig variable y-en i eit uttrykk som beskriv samanhengen mellom dei:
\(y = (x-1)\cdot 4 + 5\)
Vi kan teikne ein graf som viser denne samanhengen. Grafen hjelper oss med å finne talet på synlege sider for alle moglege talet på terningar. Men vi må vere merksame på at denne grafen berre er gyldig for heile, positive tal på x-aksen, dvs. for 1, 2, 3 osb. terningar. Punkta er merkte med x på grafen.
Viss vi reknar ut og forenklar funksjonsuttrykket får vi \(y = 4x + 1\). Vi teiknar grafen til denne funksjonen.
\(y = (x-1)\cdot 4 + 5 \\ y=4x-4+5\\ y=4x+1\)
Talet på usynlege sider kan visast med følgjande graf. Den er også gyldig berre for heile, positive verdiar av x.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Gjennom denne aktiviteten blir elevane utfordra til å leite etter mønster og beskrive dette på fleire måtar, - med ord, med eit systematisk oppsett, med algebraisk uttrykk og eventuelt med graf. Dei må gå frå å finne eit mønster gjennom systematiske undersøkingar til å generalisere resultata.
Mogleg tilnærming
La elevane arbeide i par, og sørg for at alle para har minst fem like store kubar (centikubar eller terningar).
Be dei leggje ein terning på bordet og spør kor mange sider som er synlege. Det er lett å bli samde om at det er fem sider. Be dei så setje to terningar oppå kvarandre. Kor mange sider er synlege no? Herfrå kan kvart par arbeide med terningane sine.
Oppgåva er å finne fram til mønsteret i korleis talet på synlege sider veks for kvar ny terning som blir lagd på og å beskrive dette mønsteret med ord. Utfordre elevane til å prøve å skrive dette ned på ein oversiktleg måte.
Følg med på arbeidet og samtalane i arbeidspara. Når du stoppar arbeidet for å samanfatte i fellesskap, kan fleire par fortelje korleis dei beskriv samanhengen med ord. Skriv alle forklaringane på tavla. Til dømes:
Ein elev forklarer: «Eg ser fire sider på alle treningane pluss ei ekstra side på toppen.»
Ein annan elev forklarer: «Eg ser fem sider på den øvste terningen og fire på alle dei andre.»
Det kan komme fleire forslag, alle må noterast.
Be elevane rekne ut talet på synlege sider for 5, 10 og 100 terningar med kvar av forklaringane som utgangspunkt. Gav alle forklaringane same svar?
Set opp reknestykka på tavla:
|
Tal på terningar |
Fire sider på alle terningane pluss ei ekstra side på toppen |
Fem sider på den øvste terningen og fire på alle dei andre
|
Evt. andre forklaringar |
|
\(5\) |
\(5 \cdot 4 + 1 = 21\) |
\(5 + 4 \cdot 4 = 21\) |
… |
|
\(10\) |
\(10 \cdot 4 + 1 =41\) |
\(5 + 4 \cdot 9 = 41\) |
… |
|
\(100\) |
\(100 \cdot 4 + 1 =401\) |
\(5 + 4 \cdot 99 = 401\) |
… |
|
|
|
|
|
Viss forklaringane er rette, vil dei gi same svar. Be elevane sjå på ein og ein forklaringsmodell om gongen og finne ut kva som er fast og kva som blir forandra for kvart nytt reknestykke. Kva viss talet på terningar var ukjent? Kva viss vi seier at vi har n terningar, korleis ville utrekningane ha set ut då? Få elevane med på at vi kunne ha føydd til ei siste linje i tabellen:
|
\(n\) |
\(n \cdot 4 + 1 \) |
\(5 + 4 \cdot (n-1) \) |
… |
Desse uttrykka er generelle formlar som kan brukast same kor mange terningar vi har i tårnet. Det står att å vise at dei er like. La elevane undersøkje om alle formlane kan forenklast slik at dei blir like. Dei endar sikkert opp med formelen \(4n + 1\). Eit par spørsmål til må avklarast:
- Kan ein framleis bruke ein av dei andre formlane, t.d. \(5 + 4(n – 1)\)?
- Vi seier at ein formel med ein bokstav som kan stå for mange ulike tal, er ein generell formel. Kva er fordelane med å finne generelle formlar?
I aktiviteten er det teke med eit ekstra spørsmål om å teikne ein graf som fortel samanhengen mellom talet på terningar og talet på synlege sider. Du må vurdere om dette passar inn i arbeidet på dette tidspunktet. Viss du vil vise kor mange ulike representasjonar som kan beskrive same samanheng, er det fint å også trekkje inn grafen. Men då må de samtidig ta opp at sjølv om denne grafen blir teikna som ei samanhengande linje, er den gyldig berre i dei punkta der x-verdien er eit positivt heiltal, sidan ho angir talet på terningar i tårnet.
Oppgåva med å gjere tilsvarande undersøkingar med talet på usynlege sider, blir ei gjentaking, ei øving i å gjere det same med utgangspunkt i ein litt annleis situasjon.
Gode rettleiingsspørsmål
-
Korleis tel du for å finne talet på synlege sider når du har 2 terningar, 3 terningar, 4 terningar?
-
Kan du forklare korleis ein bør telje systematisk kvar gong?
-
Kan du skrive ned korleis du har rekna ut talet på synlege sider i kvart av tilfella?
Mogleg utviding
Kanskje er det å teikne grafar ei utviding av oppgåva som ikkje alle elevane skal vere med på?
Kanskje vil nokon diskutere korleis ein skal tolke verdien der grafen skjer y–aksen, altså «talet på synlege sider er 1 viss vi har 0 terningar»? Kan dette gi meining?
Elevane kan oppmodast til å lage andre variantar av oppgåva, til dømes tårn med to og to terningar inntil kvarandre, eller andre figurar som veks etter eit gitt mønster. Så kan dei finne reglar og formlar for korleis talet på synlege sider aukar når talet på terningar aukar.
Ressursen er utviklet av Matematikksenteret