Hurra for flagget
Aktivitet
Del 1
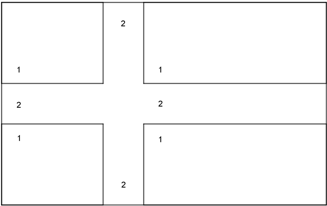
Kjenner du det svenske flagget?
Hvis vi skal fargelegge flagget, må vi farge blått i alle felt som er merket med 1 og gult der det er merket med 2.
Tenk deg nå at du har fire farger å velge mellom: Blått, gult, rødt og hvitt.
Hvor mange ulike flagg kan du fargelegge hvis du bare skal bruke to farger, og de skal farges med én farge der det står 1 og en annen farge der det står 2?
Kan du tenke det ut uten å prøve først? Hvordan tenker du da?
Du kan skrive ut Kopioriginal 1 med mange flagg som du kan fargelegge. Hvor mange ulike flagg kan du fargelegge når du bare får bruke de fire fargene? Hvordan kan du være sikker på at du har laget alle mulige kombinasjoner?
Noen av flaggene du har fargelagt, er nasjonalflagg? Kan du finne ut hvilke land de tilhører?
Del 2
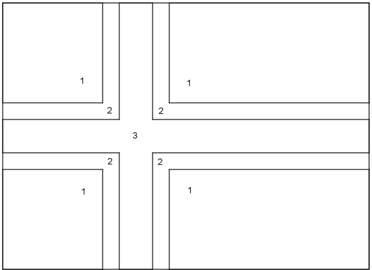
I det norske flagget er det tre farger, rødt, hvitt og blått.
Her er det rødt i alle felt som er merket 1, hvitt i feltene som er merket 2 og blått i feltet som er merket 3.
Tenk deg at du har tre farger, rødt, hvitt og blått.
På hvor mange ulike måter kan du fargelegge flagget hvis du bare har tre farger?
Kan du tenke ut hvor mange måter det blir uten å fargelegge først? Hvordan tenker du da?
Du kan skrive ut Kopioriginal 2 med flagg som du kan fargelegge. Fargelegg alle mulige kombinasjoner. Hvor mange mulige kombinasjoner ble det?
Hvordan tenkte du for å være sikker på at du laget alle mulige kombinasjoner?
Hvor mange av flaggene du har fargelagt, er flagg som er i bruk? Hvilke land har disse flaggene?
Del 3 – ekstra utfordring:
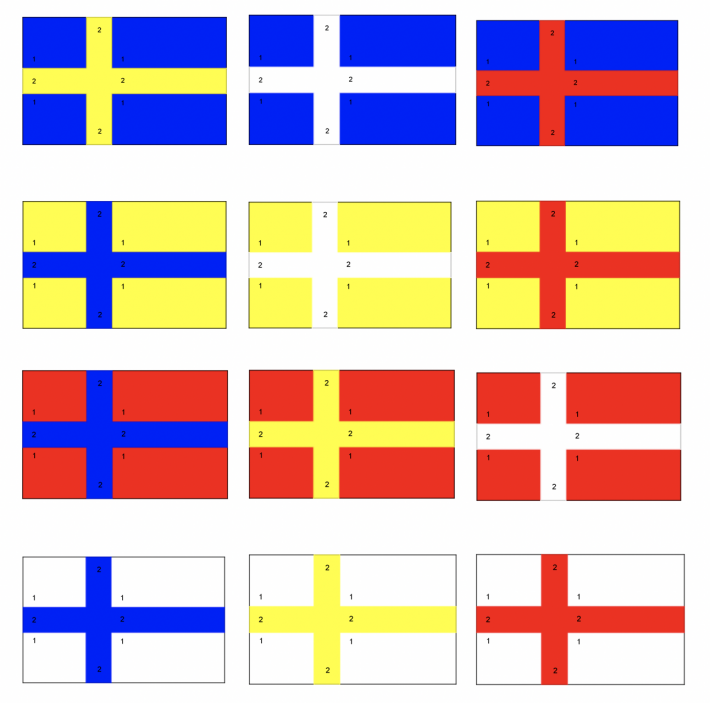
Åland har et flagg som er delt opp på samme måte som det norske, men fargene er blått, gult og rødt:
Hvor mange ulike flagg som er delt opp som det norske, kan du fargelegge hvis du kan bruke fire farger: Rødt, hvitt, blått og gult?
Starthjelp
- Hvordan vil du planlegge fargeleggingen slik at du er sikker på at du lager alle mulige kombinasjoner?
- Hvor mange mulige farger kan du bruke i feltene som er merket 1?
- Hvor mange mulige farger kan du da bruke i feltene som er merket 2?
Løsning
Del 1
Det er 12 ulike måter å fargelegge flaggene på.
I felt som er merket 1 kan vi velge mellom 4 ulike farger. Når vi har valgt en farge for felt nr.1, er det 3 mulige farger å velge i felt nr. 2.
Vi kunne ha regnet det ut uten å fargelegge først: Det er \(4\cdot 3 = 12\) ulike flagg.
Blant disse flaggene finner du flaggene til Sverige, Finland og Danmark.
Del 2
Det er 6 ulike måter å fargelegge disse flaggene på når vi kan bruke bare 3 farger.
Vi kan velge mellom 3 ulike farger i felt nr.1. For hvert av disse kan vi velge mellom 2 ulike farger i felt nr. 2. Og når vi har valgt to farger, er det bare 1 farge igjen som kan brukes i felt nr.3.
Dette kunne vi ha regnet ut slik \(3 \cdot 2 \cdot 1 = 6\).
I tillegg til det norske flagget er også Islands og Færøyenes flagg blant disse seks.
Del 3
Hvis vi skal fargelegge 3 ulike felt og kan bruke 4 ulike farger, kan vi tenke slik:
I felt 1 kan vi velge mellom 4 ulike farger. Da er det igjen 3 ulike farger til felt 2, og deretter 2 ulike farger å velge mellom til felt 3. Det blir i alt\(4\cdot 3 \cdot 2= 24\) ulike kombinasjoner.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette er et problem som handler om kombinatorikk, men med en lav inngangsterskel. Så den kan godt være en av de første introduksjonsoppgavene til slik tenkning. Alle kan fargelegge, alle kan se at det finnes ulike kombinasjoner og alle kan finne en løsning. Men gjennom dette arbeidet vil
- elevene utfordres til å arbeide systematisk
- de utfordres til å tenke over hvordan de skal sørge for å få med alle mulige kombinasjoner
- de utfordres til å forklare hvordan de har tenkt
- og de utfordres til å forstå de første regnestykkene dere gjør innenfor kombinatorikk
Mulig tilnærming
La elevene arbeide i par. Begynn med å snakke om det svenske flagget. Er det noen som vet hvordan det ser ut? Hvilke farger har det? Vis et bilde av flagget slik at alle vet hvordan det ser ut.
Den første oppgaven er å finne ut på hvor mange måter et slikt flagg kan fargelegges hvis vi kan bruke 4 ulike farger: Blått, gult, rødt og hvitt. Kan noen elever tenke seg hvor mange kombinasjoner det blir. La dem komme med forslag og forklaringer, men la svaret stå åpnet: «Nå skal vi finne ut om de har rett.»
Del ut Kopioriginal 1 slik at alle kan fargelegge. De som ønsker det må få bruke mer enn ett ark. La dem få bruke tid på jobben. Men be dem tenke over hvordan de vil sørge for at de farger alle mulige kombinasjoner. Si at du kommer til å spørre om hvordan de planla arbeidet for å vite at alle kombinasjoner ble med. Vent med å vurdere løsningene, tipse om at de mangler noen eller har laget to like flagg, til de selv får presentere løsningene sine.
Til slutt samles hele klassen for å avrunde denne oppgaven. La dem vise fram arbeidene sine. Hvor mange har de fargelagt? Har alle fargelagt like mange? Hvordan kan de være sikre på at de har laget alle kombinasjoner, - og at de ikke har laget samme kombinasjon flere ganger? La ulike forklaringen komme til orde. Hvis du har sett noen som har arbeidet veldig systematisk, kan de få slippe til sist. Ut fra en forklaring som «I felt 1 kan vi velge mellom 4 ulike farger, og da var det 3 ulike farger igjen til felt 2», er veien kort til å sette dette opp som et regnestykke: \(4\cdot 3 = 12\). Til slutt vil kanskje noen se at de mangler noen flagg som de vil supplere med, eller noen finner at de har laget flere like flagg så de har fått for mange.
Neste oppgave tar utgangspunkt i det norske flagget, med tre ulike farger. Hvor mange ulike måter kan fargene rødt, hvitt og blått kombineres i mønsteret til dette flagget? Spør igjen om noen kan tenke seg det. Få fram forslag og forklaringer, men vent med å bekrefte om noe er riktig. Gi dem en ny fargeleggingsoppgave, fra Kopioriginal 2. Hvor mange ulike flagg ble det nå? Hvordan kan de være sikre på at de har fått med alle mulige kombinasjoner? Og at de ikke har laget samme flere ganger?
Gi rom for å vise fram arbeider, diskutere og forklare. Vurder ulike strategier sammen med elevene. Er det noen som har brukt strategier som er mer effektive enn andre? Hvorfor er de effektive? Kan vi lære noe av disse? Let etter forklaringer som kan «oversettes» til et regnestykke: \(3 \cdot 2 \cdot 1 = 6\).
Den siste oppgaven er kanskje bare for noen få. Hvis noen har god tid, kan de fargelegge. Eller de kan løse problemet ved å resonnere. Du må vurdere om denne oppgaven skal tas opp i klassesamtalen.
Gode veiledningsspørsmål
- Hvordan planlegger du for å sørge for at du får med alle mulige fargekombinasjoner?
- Hvilket felt i flagget vil du fargelegge først?
- Hvor mange mulige farger kan du bruke i felt nr. 1? Hvor mange farger er det da igjen å velge mellom i felt nr.2? (og i oppgave 2: Hvor mange farger er det igjen å velge mellom til felt nr. 3?)
- Hvordan vet du at du har fargelagt alle mulige kombinasjoner?
Ressursen er utviklet av Matematikksenteret