Hurra for flagget
Aktivitet
Del 1
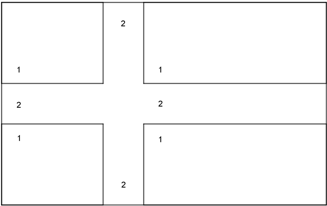
Kjenner du det svenske flagget?
Dersom vi skal fargeleggje flagget, må vi farge blått i alle felt som er merkte med 1, og gult der det er merkt med 2.
Tenk deg no at du har fire fargar å velje mellom: blått, gult, raudt og kvitt.
Kor mange ulike flagg kan du fargeleggje dersom du skal bruke berre to fargar, og dei skal fargast med éin farge der det står 1, og ein annan farge der det står 2?
Kan du tenkje det ut utan å prøve først? Korleis tenkjer du då?
Du kan skrive ut Kopioriginal 1 med mange flagg som du kan fargeleggje. Kor mange ulike flagg kan du fargeleggje når du får bruke berre dei fire fargane? Korleis kan du vere sikker på at du har laga alle moglege kombinasjonar?
Nokre av flagga du har fargelagt, er nasjonalflagg. Kan du finne ut kva land dei høyrer til?
Del 2
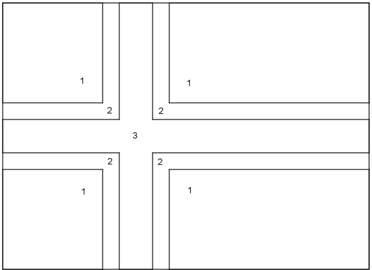
I det norske flagget er det tre fargar: raudt, kvitt og blått.
Her er det raudt i alle felt som er merkte 1, kvitt i felta som er merkte 2, og blått i feltet som er merkt 3.
Tenk deg at du har tre fargar: raudt, kvitt og blått.
Kor mange ulike måtar kan du fargeleggje flagget på dersom du har berre tre fargar?
Kan du finne ut kor mange måtar det blir utan å fargeleggje først? Korleis tenkjer du då?
Du kan skrive ut Kopioriginal 2 med flagg som du kan fargeleggje. Fargelegg alle moglege kombinasjonar. Kor mange moglege kombinasjonar vart det?
Korleis tenkte du for å vere sikker på at du laga alle moglege kombinasjonar?
Kor mange av flagga du har fargelagt, er flagg som er i bruk? Kva land har desse flagga?
Del 3 – ekstra utfordring:
Åland har eit flagg som er delt opp på samme måten som det norske, men fargane er blått, gult og raudt:
Kor mange ulike flagg som er delte opp som det norske, kan du fargeleggje dersom du kan bruke fire farger: raudt, kvitt, blått og gult?
Starthjelp
- Korleis vil du planleggje fargelegginga for å vere sikker på at du lagar alle moglege kombinasjonar?
- Kor mange moglege fargar kan du bruke i felta som er merkte 1?
- Kor mange moglege fargar kan du då bruke i felta som er merkte 2?
Løysing
Del 1
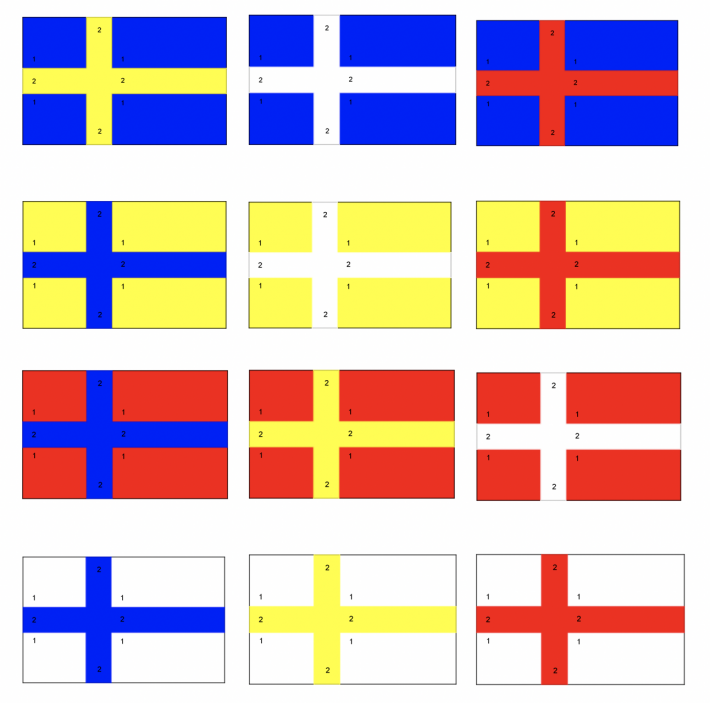
Det er 12 ulike måtar å fargeleggje flagga på.
I felt som er merkte 1, kan vi velje mellom 4 ulike fargar. Når vi har valt ein farge for felt nr. 1, er det 3 moglege fargar å velje mellom i felt nr. 2.
Vi kunne ha rekna det ut utan å fargeleggje først: Det er \(4\cdot3=12\) ulike flagg.
Mellom desse flagga finn du flagga til Sverige, Finland og Danmark.
Del 2
Det er 6 ulike måtar å fargeleggje desse flagga på når vi kan bruke berre 3 fargar.
Vi kan velje mellom 3 ulike fargar i felt nr. 1. For kvart av desse flagga kan vi velje mellom 2 ulike fargar i felt nr. 2. Og når vi har valt 2 fargar, er det berre 1 farge igjen som kan brukast i felt nr. 3.
Dette kunne vi ha rekna ut slik: \(3\cdot2\cdot1=6\).
I tillegg til det norske flagget er også flagga til Island og Færøyane mellom desse seks.
Del 3
Dersom vi skal fargeleggje 3 ulike felt og kan bruke 4 ulike fargar, kan vi tenkje slik:
I felt nr. 1 kan vi velje mellom 4 ulike fargar. Då er det igjen 3 ulike fargar til felt nr. 2, og deretter 2 ulike fargar å velje mellom til felt nr. 3. Det blir i alt \(4\cdot3\cdot2=24\) ulike kombinasjonar.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Dette er eit problem som handlar om kombinatorikk, men med ein låg inngangsterskel. Så denne oppgåva kan godt vere ei av de første introduksjonsoppgåvene til slik tenking. Alle kan fargeleggje, alle kan sjå at det finst ulike kombinasjonar, og alle kan finne ei løysing. Men gjennom dette arbeidet vil elevane bli utfordra til å
- arbeide systematisk
- tenkje over korleis dei skal sørgje for å få med alle moglege kombinasjonar
- forklare korleis dei har tenkt
- forstå dei første reknestykka dei gjer innanfor kombinatorikk
Mogleg tilnærming
La elevane arbeide i par. Begynn med å snakke om det svenske flagget. Er det nokon som veit korleis det ser ut? Kva fargar har det? Vis eit bilete av flagget, slik at alle veit korleis det ser ut.
Den første oppgåva er å finne ut kor mange måtar eit slikt flagg kan fargeleggjast på dersom vi kan bruke 4 ulike fargar: blått, gult, raudt og kvitt. Kan nokon tenkje seg kor mange kombinasjonar det blir? La elevane kome med forslag og forklaringar, men la svaret stå ope: «No skal vi finne ut om de har rett.»
Del ut Kopioriginal 1, slik at alle kan fargeleggje. Dei som vil det, må få bruke meir enn eitt ark. La dei få bruke tid på jobben. Men be dei tenkje over korleis dei vil sørgje for at dei fargar alle moglege kombinasjonar. Sei at du kjem til å spørje om korleis dei planla arbeidet for å vite at alle kombinasjonar vart med. Vent med å vurdere løysingane, tips om at dei manglar nokre eller har laga to like flagg, før dei sjølve får presentere løysingane sine.
Til slutt samlar du heile klassen for å avrunde denne oppgåva. La dei vise fram arbeida sine. Kor mange har dei fargelagt? Har alle fargelagt like mange? Korleis kan dei vere sikre på at dei har laga alle kombinasjonar, og at dei ikkje har laga den same kombinasjonen fleire gonger? La ulike forklaringar kome til orde. Dersom du har sett nokon som har arbeidd veldig systematisk, kan dei få sleppe til sist. Ut frå ei forklaring som «i felt nr. 1 kan vi velje mellom 4 ulike fargar, og då er det 3 ulike fargar igjen til felt nr. 2», er vegen kort til å setje dette opp som eit reknestykke: \(4\cdot 3 = 12\). Til slutt vil kanskje somme sjå at dei manglar nokre flagg som dei vil supplere med, eller somme finn at dei har laga fleire like flagg, så dei har fått for mange.
Neste oppgåve tek utgangspunkt i det norske flagget, med tre ulike fargar. Kor mange ulike måtar kan fargane raudt, kvitt og blått kombinerast i mønsteret til dette flagget? Spør igjen om nokon kan tenkje seg det. Få fram forslag og forklaringar, men vent med å stadfeste om noko er rett. Gi dei ei ny fargeleggingsoppgåve, frå Kopioriginal 2. Kor mange ulike flagg vart det no? Korleis kan dei vere sikre på at dei har fått med alle moglege kombinasjonar, og at dei ikkje har laga same flagg fleire gonger?
Gi rom for å vise fram arbeid, diskutere og forklare. Vurder ulike strategiar saman med elevane. Er det nokon som har brukt strategiar som er meir effektive enn andre? Kvifor er dei effektive? Kan vi lære noko av desse strategiane? Leit etter forklaringar som kan omsetjast til eit reknestykke: \(3 \cdot 2 \cdot 1 = 6\).
Den siste oppgåva er kanskje berre for nokre få. Dersom nokon har god tid, kan dei fargeleggje. Eller dei kan løyse problemet ved å resonnere. Du må vurdere om denne oppgåva skal takast opp i klassesamtalen.
Gode rettleiingsspørsmål
- Korleis planlegg du for å sørgje for at du får med alle moglege fargekombinasjonar?
- Kva felt i flagget vil du fargeleggje først?
- Kor mange moglege fargar kan du bruke i felt nr. 1? Kor mange fargar er det då igjen å velje mellom til felt nr. 2? (Og i oppgåve 2: Kor mange fargar er det igjen å velje mellom til felt nr. 3?)
- Korleis veit du at du har fargelagt alle moglege kombinasjonar?
Ressursen er utviklet av Matematikksenteret