Kvadratisk rutenett
Problem
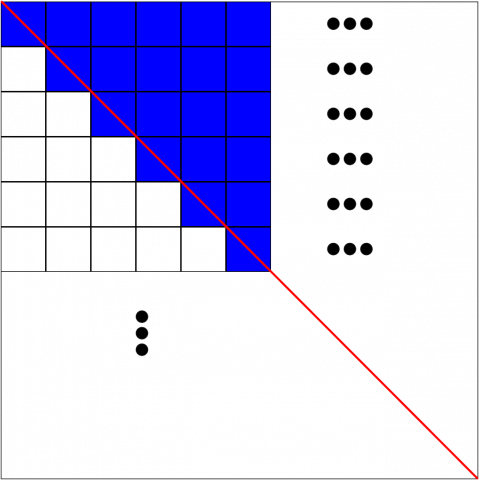
Et kvadrat er delt opp i 100 x 100 ruter. 100 ruter i første rad er fargelagt, 99 i andre rad, 98 i tredje rad, osv.
- Hvor stor brøkdel av hele det store kvadratet er fargelagt?
- Kan du forklare hvordan du kan bestemme antall fargede ruter uansett hvor stort kvadratet er
- med ord?
- med en formel?
- med en tegning?
Hva hvis det var en kube bygget opp av 100 lag med \(100\cdot100\) små kuber i hvert lag? \(99\cdot99\) fargede kuber i første lag, \(98\cdot98\) fargede kuber i andre lag, \(97\cdot97\) kuber i tredje lag og så videre.
- Hvor stor brøkdel av de små kubene er fargelagt?
Starthjelp
- Du kan tegne for å få oversikt.
- Du kan tegne et mindre kvadrat som er delt opp i ruter, og fargelegge etter samme mønster. Hvor stor del av dette kvadratet blir fargelagt?
Løsning
Det er flere måter å løse oppgaven på:
1. Sammenligne løsningen med halvparten av kvadratet
Tenk deg at du kutter kvadratet gjennom diagonalen slik figuren viser. Til høyre for diagonalen er alt fargelagt. Men det fargelagte området er større enn halvparten av kvadratet, for det er en halv fargelagt rute til venstre for diagonalen for hver rad. Det er 100 rader, og 100 halve ruter blir til sammen 50 hele ruter.
Det fargelagte området er halvparten av de 100 x 100 rutene + 50 ruter, det vil si 5000 ruter + 50 ruter = 5050 ruter.
Brøkdelen av hele kvadratet blir \(\displaystyle{5050 \over 10000 } = {101 \over 200 }\) .
2. Legge til en ekstra rad
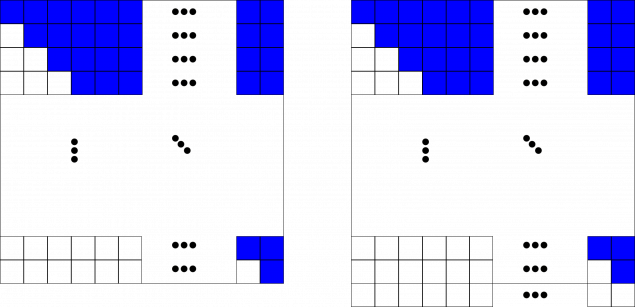
I kvadratet er det det nesten like mange hvite som fargelagte ruter. For eksempel har den tredje raden 98 fargelagte ruter, men den nest siste raden har 98 hvite ruter, se figuren til venstre. Hvis vi føyer til en ekstra rad med hvite ruter, slik figuren til høyre viser, vil det være like mange hvite som fargede ruter. I rutenettet til høyre er det 101 rader, men fortsatt 100 kolonner, så det er til sammen 100 • 101 ruter = 10 100 ruter. Halvparten av det er 5050, så 5050 av de 10 000 rutene i det opprinnelige kvadratet er fargelagt.
Brøkdelen av hele kvadratet blir \(\displaystyle{5050 \over 10000 } = {101 \over 200 }\).
3. Flytte på rader
Vi kan tenke oss at vi klipper ut de fargelagte rutene i de nederste radene og flytter dem opp til de øverste radene, slik at vi bare får rader der alle rutene er fargelagt. På figuren har de fire nederste radene blitt flyttet opp.
Hvor mange rader kan vi flytte på denne måten?
La rad 1 være nederste rad. Rad 1 er satt sammen med rad 99, rad 2 med rad 98, rad 3 med rad 97, osv., og rad 49 blir satt sammen med rad 51. Da blir rad 50 stående med 50 fargelagte og 50 hvite ruter. 50 rader har alle rutene fargelagt, og 49 rader har bare hvite ruter. I alt er 50 • 100 + 50 ruter fargelagt = 5050 ruter.
Brøkdelen av hele kvadratet blir \(\displaystyle{5050 \over 10000 } = {101 \over 200 }\) .
Ressursen er utviklet av NRICH