Multiplikasjons-aritmagonar
Aktivitet
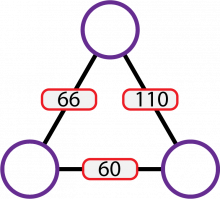
Ein aritmagon er ein polygon med tal i hjørna og ein eller fleire reglar for tala som skal vere på sidene. Vanlegvis legg vi saman tala i hjørna for å finne tala på sidene, men desse aritmagonane følgjer andre reglar. Kan du finne ut korleis tala i hjørna avgjer tala på sidene i det interaktive verktøyet under?
Dersom du kjenner verdien av tala på sidene (i dei raude boksane), kan du då lage ein regel som gjer at du kan finne ut kva for tal som skal stå i hjørna?
Bruk det interaktive verktøyet under, og test strategien din.
Det er tre nivå med ulik vanskegrad. Begynn med nivå 1.
Når du kjenner deg trygg på at du kan finne ut kva for tal som skal stå i hjørna eller på sidene, kan du svare på desse spørsmåla:
- Kan du formulere ein regel som gjer at du kan finne ut kva produkta på sidene blir, uavhengig av tala i hjørna?
- Er det ein samanheng mellom produkta i hjørna og produkta på sidene?
- Kva skjer med tala i hjørna dersom du doblar (tredoblar, firedoblar …) eitt eller fleire av tala på sidene?
- Kan du lage ein multiplikasjons-aritmagon med eitt eller fleire tal skrivne som brøk i hjørna og heile tal skrivne på sidene?
Starthjelp
- Kva samanheng er det mellom produktet av tala på sidene og produktet av tala i hjørna?
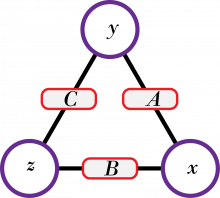
- De kan løne seg å setje namn på tala i hjørna, for eksempel A, B og C, og uttrykkje sidene ved hjelp av dei.
- Kall tala i hjørna x, y og z, og produkta på sidene A, B og C. Kva er samanhengen mellom \(A\cdot B\cdot C\) og \(x\cdot y \cdot z\)? Korleis kan du bruke denne samanhengen til å bestemme verdiane til x, y og z når du kjenner verdiane til A, B og C?
Løysing
Tala på sidene er produktet av tala i hjørna. Dersom vi tek produktet av eit tal to gonger og finn kvadratrota av talet, kjem vi tilbake til utgangspunktet. Det same vil også skje her. Tek vi produktet av tala på sidene, har vi teke produktet av tala i hjørna to gonger. Kvadratrota vil difor gi oss produktet av tala i hjørna.
Ettersom vi no har produktet av tala i hjørna, kan vi finne kvart enkelt tal ved å dividere produktet med tala på sidene, fordi tala på sidene er produktet av tala i hjørna.
Eksempel:
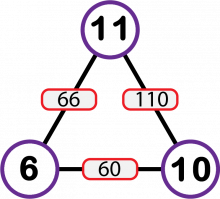
\(\begin{align}66\cdot110\cdot60&=435\:600\\ \sqrt{435\:600}&=\pm 660\\ \\ 660:66&=10 & (-660):66&=-10\\ 660:110&=6 \qquad\lor &(-660):110&=-6\\ 660:60&=11 &(-660):60&=-11\end{align}\)
Vi kan sjå på dette generelt ved å la x, y og z vere hjørna og A, B og C vere sidene. A, B og C er produkt av xy, xz og yz.
Når \(A=xy,\:B=xz\:og\:C=yz\:\:\:\Rightarrow\:\:\:y=\frac Ax\land\:z=\frac Bx\)
Vi kan dermed løyse likninga og finne x:
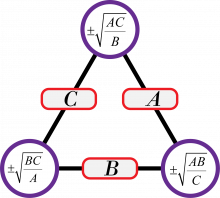
\(\begin{align} yz&=\frac{AB}{x^2}\\ x^2yz&=AB\\ Cx^2&=AB\\ x^2&=\frac{AB}C\\ x&=\pm\sqrt{\frac{AB}C} \end{align}\)
Vi gjer det same for å finne y og z:
\(y=\pm\sqrt{\frac{AC}B}\:\:\:\:\land\:\:\:\: z=\pm\sqrt{\frac{BC}A}\)
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
I denne aktiviteten får elevane høve til å utforske numeriske relasjonar algebraisk. Dei kan også arbeide med å generalisere løysingsstrategiane sine og deretter teste om dei stemmer.
Mogleg tilnærming
Dersom elevane har tilgang til PC eller nettbrett, kan dei bruke det interaktive verktøyet til å utforske multiplikasjons-aritmagonar og finne ut kva samanheng det er mellom tala på sidene og tala som skal stå i hjørna.
Alternativt kan elevane lage sine eigne multiplikasjons-aritmagonar. Så kan dei gi ein medelev tala som skal stå på sidene, og sjå om han eller ho kan finne ut kva for tal som skal stå i hjørna. Begynn med tal frå 1 til 12, utvid deretter til 20–100, og utfordre elevane til å lage multiplikasjons-aritmagonar med brøk eller desimaltal.
Når elevane har fått god tid til å løyse fleire multiplikasjons-aritmagonar, kan du samle dei for å dele strategiane dei brukte.
Spør deretter: «Kan de sjå ein samanheng mellom produktet av dei tre tala på sidene og produktet av tala i hjørna?» Dersom elevane ikkje har tenkt på denne problemstillinga, bør dei få nokre minutt til å sjå på nokre eksempel. Oppfordre dei til å bruke algebra til å beskrive den generelle samanhengen dei legg merke til.
Når elevane har kome fram til ein effektiv metode som fungerer for alle multiplikasjons-aritmagonar, kan du samle dei for å teste ut metodane på vanskelege multiplikasjons-aritmagonar som dei har brukt lang tid på å løyse tidlegare. Det er for å sjå kor kraftfull ein generell regel kan vere.
Til slutt kan elevane reflektere over desse spørsmåla på bakgrunn av det dei har lært om algebraisk tenking og generalisering:
- Kva kriterium må liggje til grunn for tala på sidene for at tala i hjørna skal vere heile tal?
- Kva skjer med tala i hjørna dersom du doblar (tredoblar, firedoblar …) eitt eller fleire av tala på sidene?
- Kan du lage ein multiplikasjons-aritmagon med eitt eller fleire tal skrivne som brøk i hjørna og heile tal skrivne på sidene?
Gode rettleiingsspørsmål
- Er det alltid mogleg å finne tala i hjørna, same kva for tal det er på sidene?
- Kva er samanhengen mellom produktet av tala på sidene og produktet av tala i hjørna?
Mogleg utviding
- Kan du lage ein multiplikasjons-aritmagon der tala i hjørna er irrasjonale, samtidig som tala på sidene er rasjonale?
- Kan du lage ein multiplikasjons-aritmagon der berre eitt eller to av tala i hjørna er irrasjonale, samtidig som tala på sidene er rasjonale?
Ressursen er utviklet av NRICH