Finn det ukjende talet
Aktivitet
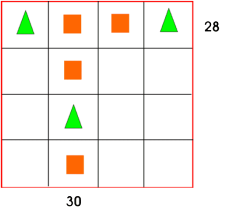
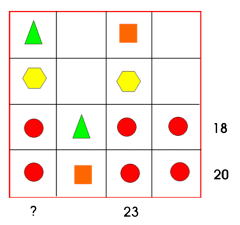
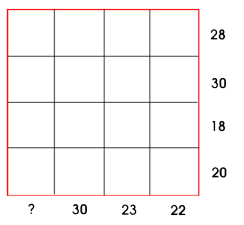
I biletet nedanfor står kvar figur for eit heilt tal. Summen av tala er skriven i enden av kvar rad og kvar kolonne.
Finn talet som skal stå på plassen til spørsmålsteiknet.
Det er mykje informasjon i rutenettet, så de må bestemme dykk for kva de vil begynne å fokusere på. Nedanfor er det nokre figurane som kan hjelpe dykk med å sjå på ein spesiell del av informasjonen i rutenettet.
- Kva kan de finne ut frå kvart av bileta nedanfor?
- Kan de finne fleire måtar å løyse dette problemet på?
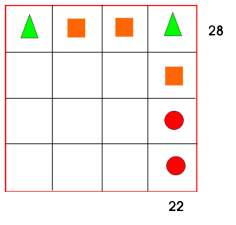
Bilete 2
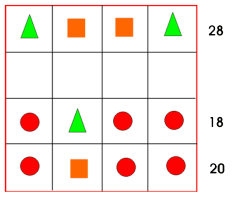
Bilete 3
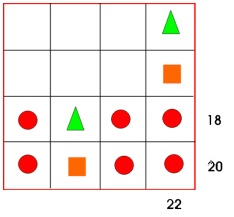
Bilete 4
Bilete 5
Bilete 6
De kan bruke dei same strategiane til å løyse tilsvarande problem. I reknearket de finn her, er det mange eksempel.
Starthjelp
- Kva kan de finne ut dersom de samanliknar dei to nedste rekkjene?
- Dersom de har funne verdien som kvadratet står for, korleis kan de då finne verdien som trekanten står for?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Oppgåva er ei god utfordring når det gjeld å resonnere dersom det er mange ukjende. Enkelte oppgåver gir meir informasjon enn nødvendig, og ein kan reflektere over kor mykje informasjon som er nødvendig og tilstrekkeleg.
Dette er ei prealgebraoppgåve som kan brukast til å introdusere metodane vi nyttar når vi løyser likningssystem.
Mogleg tilnærming
Oppgåva kan skrivast ut på ark til elevane, eller berre visast på tavla. Kopieringsoriginal til oppgåva finst her.
I tabellen i oppgåva står kvar figur for eit heilt tal. Summen av tala er skrivne i enden av kvar rad og kvar kolonne.
«Dette er eit verkeleg interessant problem, for det kan løysast på mange forskjellige måtar. Kan de finne talet som manglar, summen av tala som skal stå i den venstre kolonnen?»
«Kan de finne fleire måtar å løyse oppgåva på?»
Etter at elevane har brukt nokre minutt på oppgåva, kan dei få sjå ulike tips til korleis dei kan begynne å løyse henne. Kopieringsoriginalane som ligg her, inneheld seks bilete, hjelpefigurar, med forslag til ulike måtar å begynne på.
«Det er mykje informasjon i tabellen i oppgåva, så de må bestemme dykk for kva de vil begynne med, og kva de vil finne ut først. Kvar hjelpefigur fokuserer på ein bestemt del av rutenettet. Kva kan kvar av hjelpefigurane hjelpe dykk med å finne ut? Korleis kan dei til saman hjelpe dykk med å løyse heile oppgåva?»
Hjelpefigurane er skrivne ut på to ark, og læraren kan la halve klassen arbeide med det eine og den andre halvdelen med det andre.
«Om ei stund vil eg be nokre av dykk kome til tavla og presentere favorittmetoden dykkar for å løyse oppgåva. Så gjer deg klar til å forklare kvart steg i det du har tenkt, klart og tydeleg, og grunngi kvifor dette vart favorittmetoden din.»
Dersom nokon står fast, kan det vere nyttig å spørje:
«Kva kan du finne ut ved å samanlikne dei to nedste radene?»
«Dersom de kan finne tala i denne rekkjefølgja: kvadrat, sekskant, sirkel, trekant – korleis kunne de då ha funne løysingane i denne rekkjefølgja: trekant, sirkel, sekskant, kvadrat?»
Sørg for at elevane i løpet av økta har fått sjå og høyre mange ulike måtar å resonnere og finne løysingar på.
Mogleg utviding
I reknearket som finst her, kan det genererast mange tilsvarande oppgåver.
Dette arket har berre tabellar med figurane innteikna, men det er plass til å lage nye oppgåver ved å fylle ut ulike tal utanfor radene og kolonnane.
Ressursen er utviklet av NRICH