Leik i hagen
Aktivitet
Mona og Anne-Mari liker å leike i hagen til bestemor. Hagen har mange stiar med gras mellom, og liknar litt på biletet under.
Ein dag fann Mona og Anne-Mari opp ein ny leik. Reglane er slik:
- For kvar grasflekk dei løp forbi når dei løp til høgre, måtte dei leggje til eitt poeng.
- For kvar grasflekk dei løp forbi når dei løp til venstre, måtte dei trekkje frå eitt poeng.
- For kvar grasflekk dei løp forbi når dei løp framover, måtte dei leggje til to poeng.
- For kvar grasflekk dei løp forbi når dei løp bakover, måtte dei trekkje frå to poeng.
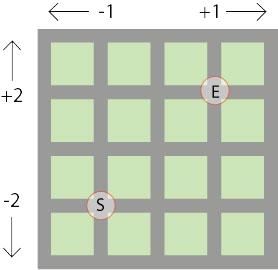
Mona og Anne-Mari starta på punktet S og slutta på punktet E på biletet under. Dei hadde 10 poeng då dei starta, og la til og trekte frå poeng etter kvart som dei valde ein veg til punktet E.
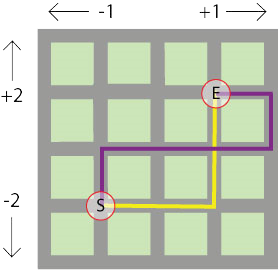
Her ser du kva vegar dei tok.
Mona valde den lilla løypa, medan Anne-Mari valde den gule løypa.
Kor mange poeng hadde Mona då ho kom fram til punktet E?
Kor mange poeng hadde Anne-Mari då ho kom fram til punktet E?
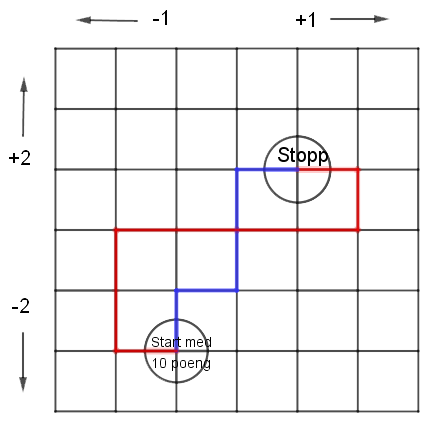
Nedanfor har vi teikna eit ruteark. Vi har teke bort graset og vegane, men vi tenkjer oss at dei kvite kvadrata er grasa, og at strekane er vegane.
Vi har teikna inn to nye vegar, ein raud og ein blå.
Kor mange poeng vil du ha til slutt viss du vel den raude vegen?
Kor mange poeng vil du ha til slutt viss du vel den blå vegen?
Lag nokre nye vegar, og rekn ut kor mange poeng du har igjen for kvar rute du lagar. Legg du merke til noko spesielt? Kan du forklare kvifor det blir slik?
Du kan laste ned kopioriginal av rutearket her.
Starthjelp
-
Forsøk å gå vegen sjølv med ei brikke. Start med 10 poeng. Gjer utrekningar for kvart steg du tek undervegs, for at det skal bli lettare å halde orden på poengsummen.
-
Korleis kan du halde orden på vegane du har gått, så du ikkje gløymer kvar du har gått?
-
Korleis skal du halde orden på poengsummen for kvar gong?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne aktiviteten vil gi elevane høve til å generalisere og laga hypotesar om kva som kjem til å skje, og kvifor. Aktiviteten gjer også at elevane får øving i enkel addisjon og subtraksjon. Den synleggjer dei inverse relasjonane mellom dei to operasjonane, og motiverer elevane til å tenkje på rekkjefølgja til operasjonane.
Mogleg tilnærming
Her kan du hente ein kopioriginal til aktiviteten.
Ein måte å introdusere oppgåva på er å vise det første biletet til heile klassen på ein smartboard, for å vere sikker på at alle elevane forstår leiken som Mona og Anne-Mari har laga. Viss det er mogleg, kan hagen med stiane og graset lagast med tape i klasserommet, eller i skulegarden, så elevane kan gjere leiken sjølv.
Etter introduksjonen kan elevane arbeide saman i par med oppgåvene på ein kopioriginal. Når dei arbeider i par, får dei høve til å diskutere løysingsforslaga sine med kvarandre. Oppmod elevane til å lage ulike løyper med både addisjon og subtraksjon. Dei kan teikne inn rutene med ulike fargeblyantar, men det kan bli mange ruter, så dei kan komme til å trenge fleire kopioriginalar. For nokre elevar kan det vere nyttig å ha konkretar tilgjengeleg når dei skal addere og subtrahere poeng.
Når elevane har arbeidd med oppgåvene, kan elevpara dele løysingane og strategiane sine i plenum. Dei kan vise dei mest interessante og lengste rutene, og kva dei har lagt spesielt merke til. Utfordre elevane på om det er nokon som kan forklare kvifor det blir den same poengsummen, uansett kva rute ein vel, så lenge startpunktet og sluttpunktet er det same.
Gode rettleiingsspørsmål
-
Korleis kan du halde styr på kva ruter du har prøvd ut?
-
Korleis skal du hugse poengsummen for kvar rute du prøver?
-
Kan du finne ein meir spennande veg å gå?
-
Kan du sjekke poengsummen på ein annan måte?
-
La du merke til noko spesielt med den totale poengsummen?
Ressursen er utviklet av NRICH