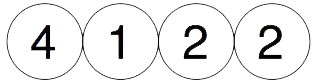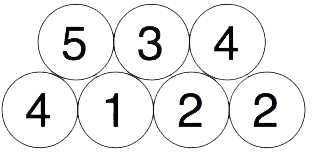Taltårn
Aktivitet
Vi startar med fire tilfeldige tal, men ikkje 0.
Så legg vi saman tala parvis og plasserer dei nye tala over, slik:
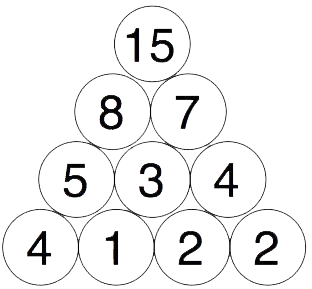
Deretter legg vi saman dei nye tala parvis og plasserer dei nye tala over på same måte, slik:
Til slutt legg vi saman dei to siste tala og plasserer det siste talet på toppen, slik:
-
Vel fire nye tal som gjer at talet på toppen blir 15.
-
Finn så mange døme på fire starttal du greier, som gjer at talet på toppen blir 15.
-
Finn du eit system? Kan du beskrive det?
-
Kvar kan det lønne seg å starte?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva utfordrar elevane til å vere kreative matematikarar. Dei må leite etter mønster og system, lage hypotesar og kontrollere dei, og dei må bruke det dei allereie kan, i nye samanhengar. Kreative matematikarar prøver seg fram med døme, teiknar, eksperimenterer og stiller gode spørsmål.
Mogleg tilnærming
Denne aktiviteten fungerer både i individuelt arbeid og som gruppearbeid, men vi tilrår at elevane får høve til å dele og diskutere løysingar med kvarandre.
Ein måte å organisere aktiviteten på er å introdusere oppgåva felles for alle elevane, til dømes på smartboard. Det er viktig at dei noterer ned svara dei finn og strategiane dei bruker. Kopioriginalar til å fylle ut tal finn du her.
Etter at elevane har arbeidd ei stund med oppgåva, bør dei få høve til å diskutere med kvarandre. Plasser dei i grupper på 2–3 elevar. Viss dei allereie har arbeidd i grupper, kan du la dei diskutere vidare. Rettleiingsspørsmåla kan vere til hjelp vidare i arbeidet.
Sett av tid på slutten av timen til å løfte fram løysingar og strategiar i plenum. Skriv dei opp slik at dei blir tilgjengelege for alle elevane. Diskuter likskapar og forskjellar i løysingane.
Ein diskusjon som kan dukke opp i gruppene og i plenum, er når to løysingar har like tal, berre på ulik plass, til dømes:
Det er ikkje eit rett eller feil svar i dette tilfellet, men det er eit døme på at det ofte må bestemmast eit kriterium for opne oppgåver som denne.
Gode rettleiingsspørsmål
-
Kva har de funne ut? Har de eit system?
-
Er det noko spesielt med dei fire tala nedst? Er det nokre tal som går igjen? Kvifor er det slik?
Mogleg utviding
-
Kan du lage tårn med andre reknereglar? Kva skjer om det er lov å bruke 0? Kva med negative tal?
-
Lag eit tårn med 5, 6, 7 … tal nedst.
Ressursen er utviklet av NRICH