Magiske bokstavar
Aktivitet
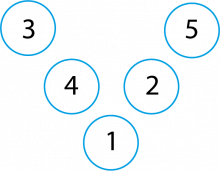
Charlotte har laga ein magisk V med fem etterfølgjande tal:
Det er ein Magisk V, for når du legg saman tala i kvar «arm» får du den same summen.
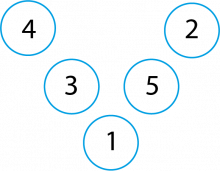
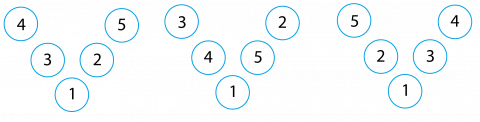
Arne teikna ein slik Magisk V:
Charlotte sa: «Det er eigentleg den same som min Magiske V!»
Kva trur du Charlotte meinte med dette?
-
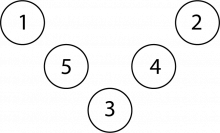
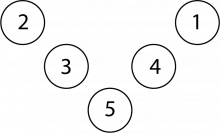
Kan du finne alle moglege Magiske V-ar som bruker tala 1 til 5 som er ulike frå Charlottes?
-
Korleis kan du vere sikker på at du har funne alle?
-
Kva skjer om du bruker tala frå 2 til 6?
-
Eller frå 3 til 7?
-
Eller 4 til 8…?
Her er eit rekneark som kan hjelpe deg med å undersøkje Magiske V-ar med fem etterfølgjande tal.
-
Kan du beskrive ein effektiv strategi for å finne alle magiske V-ar for fem kva som helst etterfølgjande tal ?
-
Kan du bruke strategien din til å finne alle moglege magiske V-ar som bruker tala 987, 988, 989, 990, 991?
-
Kan du finne ein Magisk V der kvar «arm» har sum lik 60? Eller 1000? Eller…?
-
Kan du finne meir enn éin?
-
Kan du finne ein Magisk V for alle moglege «armsummar»?
Charlotte og Arne teikna nokre fleire bokstavar, for å sjå om dei kunne gjere dei magiske; dvs. å bruke etterfølgjande tal for å lage like summar på «armane». Magisk L, N og W:
-
Utforsk nokon av desse magiske bokstavane på same måte som du utforska den magiske V.
-
Kan du finne nokon generelle konklusjonar?
Du kan bruke dette reknearket til å utforske magiske L, N og W.
Starthjelp
Kva legg du merke til når det gjeld talet som står nedst i dei magiske V-ane?
Løysing
Det er seks moglege løysingar av magisk V når vi bruker tala frå 1-5 og lèt 1 stå nedst. Alle desse er same løysing som Charlotte si:
Sidan summen av tala 1 + 2 + 3 + 4 + 5 = 15, må eit oddetal stå nedst. Viss vi set eit oddetal nedst, vil summen av dei andre tala bli eit partal, og det kan delast i to like summar. Men viss vi set eit partal nedst, vil summen av dei andre tala bli eit oddetal som aldri kan delast i to like tal.
Viss vi set 3 nedst får vi ei løysing som kan ordnast på seks ulike måtar slik som i dømet ovanfor med 1 nedst:
Viss vi set 5 nedst får vi ei løysing som også kan ordnast på seks ulike måtar slik som i dømet ovanfor:
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva gir elevane øving i å oppfatte ein struktur i eit enkelt tilfelle og generalisere løysingane ut frå strukturane dei har funne.
Mogleg tilnærming
Begynn med å teikne 5 sirklar slik at dei dannar ein V og be elevane gjere det same og prøve å plassere tala 1-5 i kvar sin sirkel. Dei kan setje tala i dei sirklane dei sjølv ønskjer.
La elevane vise fram løysingane sine og del tavla i to, med overskriftene «Magisk» og «Ikkje magisk». Vel nokre av løysingane som elevane har laga, og teikn dei opp på tavla i dei to ulike kategoriane utan å fortelje kva som gjer nokre «magiske» og andre ikkje. Utfordre elevane til å finne ut kva som gjer ei løysing «magisk».
Når elevane har funne ut kva som gjer ein V «magisk», må det gjerast klart kva som gjer to løysingar ulike, og kvifor til dømes dei tre løysingane nedanfor er like:
Arbeid til dykk har funne alle moglege løysingar (det er tre ulike løysingar, med høvesvis 1, 3 eller 5 nedst).
Ta dykk tid til å diskutere kvifor de kan vere sikre på at det ikkje finst fleire løysingar. Kva skjer når det står eit oddetal nedst i V-en, og kva skjer når det står eit partal?
La elevane no løyse ei tilsvarande oppgåve med tala 2-6. Kan dei bruke same strategi som fungerte i den første oppgåva? Kom med gode rettleiingsspørsmål som hjelper elevane på vegen til å løyse problemet sjølv.
Legg merke til elevar som finn effektive løysingsstrategiar. La dei få vise strategiane sine og forklare korleis dei har tenkt.
La elevane holde fram med å arbeide i par med fleire magiske V-ar:
-
Bruke tala frå 3 til 7
-
Bruke tala frå 4 til 8
-
Kan du beskrive ein effektiv strategi for å finne alle magiske V-ar for fem kva som helst etterfølgjande tal?
-
Kan du bruke strategien din til å finne alle moglege magiske V-ar som bruker tala 987, 988, 989, 990, 991?
-
Kan du finne ein Magisk V der kvar «arm» har sum lik 60? Eller 1000? Eller…?
-
Kan du finne meir enn éin?
-
Kan du finne ein Magisk V for alle moglege «armsummar»?
Gode rettleiingsspørsmål
-
Kva vart summen langs kvar side når vi brukte tala 2-6?
-
Kvifor blir summen langs kvar side av V med 2 i botnen 3 større enn om vi har 1 i botnen?
-
Kva er spesielt med summen langs kvar side viss talet i botnen er det midtarste av fem etterfølgjande tal?
Her finn du ein kopioriginal, ei side med magisk V og ei side med magisk L, N og W.
Her finn du rekneark for å utforske Magisk V.
Mogleg utviding
Oppgaven kan utvidast med Magisk L, N og W. Dei kan utforskast på tilsvarande måte. Ha fokus på å finne gode strategiar.
Her finner du rekneark for Magisk L, N og W.
Ressursen er utviklet av NRICH