Magisk kvadrat
Problem
Løysing
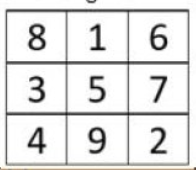
Dette er ei mogleg løysing, men det finst fleire:
Summen av alle korkane frå 1 til 9 er 45. Dersom vi deler 45 på 3 rader/kolonnar, finn vi at kvar rad/kolonne må ha summen 15.
5 må liggje i midten fordi det er det einaste talet med 4 kombinasjonsmoglegheiter som gir 15.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
I denne aktiviteten er det magiske kvadratet ein kontekst der elevane får høve til å øve hovudrekning, først og fremst addisjon, og det å arbeide systematisk. Dei får også moglegheit til å resonnere over løysingar som ikkje fører fram.
Mogleg tilnærming
Denne aktiviteten kan introduserast ved å vise biletet for alle elevane.
Be elevane tenkje individuelt over kvar dei kan begynne. Deretter skal dei diskutere ideane sine med ein medelev. Diskuter til slutt i heile klassen.
Summen av alle siffera er eit nøkkelelement i denne oppgåva, og utfordringa er korleis denne summen kan brukast for å løyse oppgåva. Sjå etter gode strategiar som tek utgangspunkt i summen av alle siffera.
Gode rettleiingsspørsmål
Ver litt sparsam med rettleiingsspørsmåla. La elevane streve før du stiller slike spørsmål!
- Korleis kan du begynne, og kvifor?
- Korleis kan du bruke løysingsforslaga som ikkje gav rett løysing, i arbeidet vidare?
- Korleis kan du halde god oversikt over det du har prøvt / funne ut?
- Kva blir summen dersom du legg saman alle tala?
- Kan du bruke denne informasjonen i arbeidet vidare?
- Kva blir summen i kvar rad/kolonne? Korleis kan denne summen vere til hjelp?
Kor mange ulike kombinasjonar gir denne summen?
Mogleg utviding
Bruk tala frå 2 til 10 og lag eit nytt magisk kvadrat.
Utvid kvadratet til 4 x 4 ruter, og bruk 16 korkar.
Mogleg støtte
Begynn med å spørje kva totalsummen på alle mjølkekorkane. Deretter kan elevane prøve å finne ut kva sum kvar rad/kolonne må ha dersom alle skal ha same summen.
Kva for talkombinasjonar gir summen 15?
Kva for ruter i 3 x 3-kvadratet blir «nytta» flest gonger? Kva for ruter blir «nytta» minst? Ut frå det, kvar er det best å plassere dei høgaste og dei lågaste tala?
Denne informasjonen kan elevane bruke når dei skal leggje kvadratet.
Ressursen er utviklet av Matematikksenteret