Nedanfor ser du ein tabell med tala 1 – 100, eit «hundrekart».
Fire ruter som dannar eit kvadrat, er markert med raudt. Bruk dei fire tala til å lage eit reknestykke etter eit bestemt mønster:
Tala som dannar ein diagonal frå øvre høgre til nedre venstre hjørne blir multiplisert med kvarandre. Trekk så frå produktet av tala i den andre diagonalen.
I dei raude rutene blir reknestykket: \(2\cdot 11-1\cdot 12\)
Kva vart svaret?
Så vel du kvadratet med dei fire lyseblå rutene og lagar eit reknestykke etter same mønster. Kva vart svaret der?
Vel fleire kvadrat med fire ruter på andre stader i hundrekartet og gjer tilsvarande utrekning. Kva blir svaret?
Du finn eit hundrekart som kan skrivast ut i menyen til venstre. Du kan leggje brikker i rutene for reknestykka du lagar, slik at arket kan brukast fleire gonger.
Kva er samanhengen mellom svara du får? Kvifor blir det slik?
Hald fram med å undersøkje reknestykke du får ved å markere kvadrat i hundrekartet, slik vi har vist med 3 x 3-ruter, 4 x 4 -ruter osb. slik figuren antydar. Bruk tala i hjørna. Marker kvadrat av same storleik fleire stader i hundrekartet og regn heile tida etter same mønster som ovanfor.
Eit skjema kan vere til hjelp:
| Storleiken på kvadratet som blir markert |
Svaret på reknestykket som er laga av tala i hjørna etter mønsteret: |
| 2 x 2 | |
| 3 x 3 | |
| 4 x 4 | |
| 5 x 5 | |
| 6 x 6 | |
| 7 x 7 | |
| 8 x 8 | |
| 9 x 9 | |
| 10 x 10 |
Fant du eit mønster som var slik at du visste kva som vart svara for kvadrata du ikkje hadde rekna ut? Kan du beskrive mønsteret? Kan du forklare kvifor det blir slik?
Du kan markere figurar som ikkje er kvadrat, lage ein rekneregel og undersøkje om du kan finne fleire mønster i hundrekartet.
Kva vil du undersøkje?
Legg ein plan, kva figurar kan du lage i staden for kvadrat? Kva rekneregel skal gjelde? Undersøk systematisk. Finn du fleire mønster? Kan du forklare kvifor mønstera blir som dei blir? Kan du vere sikker på at mønstera du vel, vil gi dei same svara same kvar i hundrekartet du markerer figuren?
Kan du lage fleire kvadrat og rekne ut på same måte? Kva ser du?
Vil det alltid bli slik med 2 x 2-kvadrat? Kvifor?
Kva er samanhengen mellom dei fire tala du bruker i reknestykket?
Korleis er denne samanhengen for 2 x 2-kvadrat på ulike stader i hundrekartet?
I denne oppgåva skal elevane først eksperimentere og finne mønster. Det er ei fin oppgåve for å vise korleis vi generaliserer ved hjelp av algebra.
La elevane samarbeide i par.
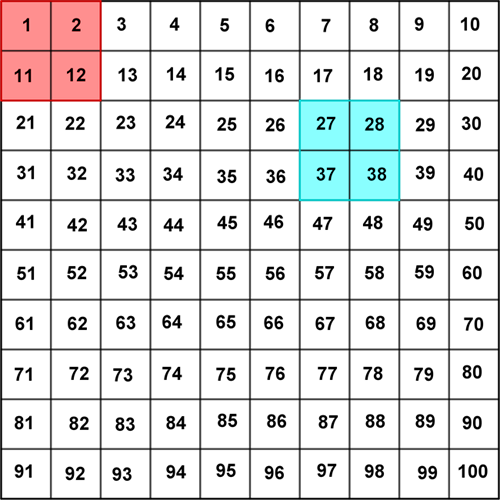
La dei få eit «hundrekart» å arbeide med, det finst på kopioriginal i menyen til venstre, saman med teljebrikker eller noko som kan leggjast som markering i rutene på arket. Be elevane markere dei fire rutene som dannar eit 2 x 2-kvadrat øvst i venstre hjørne (1, 2, 11, 12) og be dei rekne etter mønsteret som er angitt i oppgåva:
\(\text{øvre høyre}\cdot\text{nedre venstre}-\text{øvre venstre}\cdot\text{nedre høyre}\).
Sørg for at alle forstår korleis vi set opp reknestykket, for det skal dei bruke mange gonger i denne aktiviteten. Kva blir svaret? Fekk alle det same?
Be elevane halde fram med å markere rutene 27, 28, 37, 38 og rekne ut på tilsvarande måte her. Kva blir svaret no? Er det nokon som trur dei kan finne fleire stader i hundrekartet der dei vil få same svar? La dei prøve ei stund (berre med 2 x 2-ruter). Når alle har fått tid til fleire forsøk, er det tid for å diskutere i fellesskap: Vil det bli same svar same kvar vi plasserer kvadratet?
Kan nokon forklare kvifor? Slepp til alle forklaringar dei kan komme med, men la det i første omgang stå ope kva som er rett og gale. No skal elevane takast med i tenkinga som ligg bak ei generalisering: Be dei markere 2 x 2-kvadrat på to ulike stader i hundrekartet:
Sjå på dei to øvste tala i dei to markerte felta: Kva er likt, kva har dei til felles? Kan alle sjå at same kvar dei markerer vil det andre talet vere 1 større enn det første?
No kan du innføre bokstavar for tal: Vel ein bokstav, til dømes a. Viss talet øvst til venstre i ruta er a, kva er då talet øvst til høgre? (a + 1)
Så kan dei samanlikne dei to markerte kvadrata på nytt, sjå på tala øvst til venstre og nedst til venstre: Har desse to tala noko til felles i dei to markerte rutene? Kan alle sjå at same kvar vi plasserer eit 2 x 2-kvadrat vil det nedste talet vere 10 større enn det øvste? Korleis kan vi skrive dette talet på algebraspråket? (a + 10)
Korleis kan vi då skrive talet nedst til høgre i 2 x 2-kvadratet? Få alle med på at dette blir a + 11.
Det betyr at alle 2 x 2-kvadrat kan skrivast på same måte:
| \(a\) | \(a+1\) |
| \(a+10\) | \(a+11\) |
Skriv dette opp på tavla og be elevane rekne ut etter same mønster som før. Kva ser dei? Kva blir svaret?
No kan de gå tilbake til forklaringane elevane hadde komme med: Var dei i samsvar med det vi gjorde her? Var noko ulikt, evt. kva? Var det nokon som ønskte å endre forklaringa si fordi dei hadde misforstått noko? Kva hadde dei misforstått?
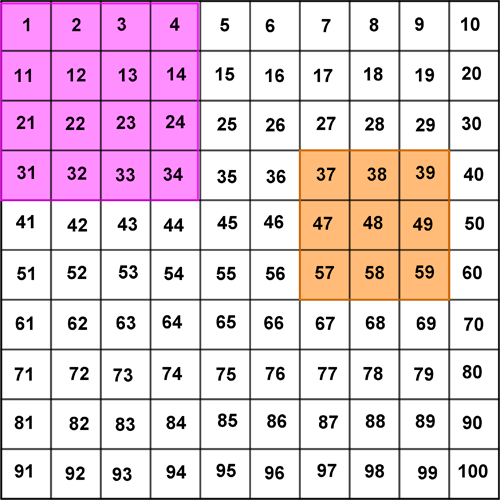
Viss de arbeider grundig med denne første delen av oppgåva, kan elevane arbeide meir sjølvstendig med fortsetjinga: Marker kvadrat med andre storleikar i hundrekartet, 3 x 3, 4 x 4 osb. Be dei notere storleiken på kvadrata og svaret på utrekningane, bruk alltid tala i hjørna av kvadrata og følg same regel som før. Kan dei finne eit system i svara ettersom dei gjer kvadrata gradvis større? Kan dei finne ei forklaring på korleis desse svara utviklar seg? Kan dei finne ein generell samanheng eller regel?
Bruk tid på å samanfatte og ha spesielt fokus på generaliseringane. Sørg for at dei kan forklarast både med ord og med symbol.
I det vidare arbeidet er det ope for meir utforsking. Elevane kan komme med forslag til kva slags figurar i hundrekartet dei vil utforske og kva rekneregelen skal vere. Det enklaste er nok å halde fram med rektangel. De kan anten bli samde om éi oppgåve som alle arbeider vidare med, eller du kan la kvart arbeidspar arbeide med eigne idear. I så fall må dei lage ein skriftleg rapport som fortel kva figur dei har valt i hundrekartet, kva som er rekneregelen, kva døme på utrekning dei har prøvd og korleis dei har generalisert resultatet. Det kan hende nokon lagar figurar og reknereglar som ikkje gir same svar gjennom heile hundrekartet. I tilfelle er det ei fin oppgåve å utfordre elevane til å finne ut kvifor. Det er fint om slike rapportar over arbeidet i dei enkelte para kan bli synlege for alle til slutt.
Kan du lage fleire kvadrat og rekne ut på same måte? Kva ser du?
Vil det alltid bli slik med 2 x 2-kvadrat? Kvifor?
Kva er samanhengen mellom dei fire tala du bruker i reknestykket?
Korleis er denne samanhengen for 2 x 2-kvadrat på ulike stader i hundrekartet?
Oppgåva kan utvidast i mange retningar idet ein lèt elevane sjølv velje figurar i hundrekartet som skal utforskast, og kva reknereglar som skal gjelde.
Ressursen er utviklet av Matematikksenteret
