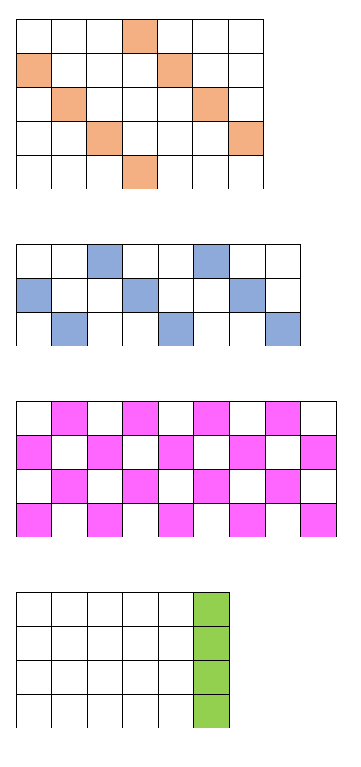
Elleville mønster
Aktivitet
Mange har sikkert prøvd å lage mønster i 100-kartet (rutenettet med 10 x 10 ruter). Når vi bruker multiplikasjonstabellane som utgangspunkt for mønster, kan vi finne mønster med vertikale og diagonale linjer, og nokre mønster som gjentek seg over heile rutenettet. I dette problemet vil vi kalle 100-kartet tiar-kartet. Viss kartet har 9 x 9 ruter, vil vi kalle det niar-kartet, osb.
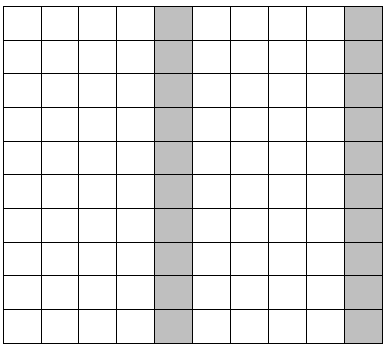
Kva tal kan ha laga mønstera ovanfor?
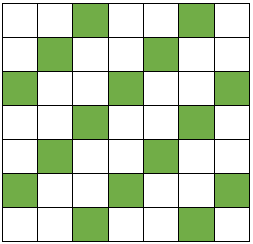
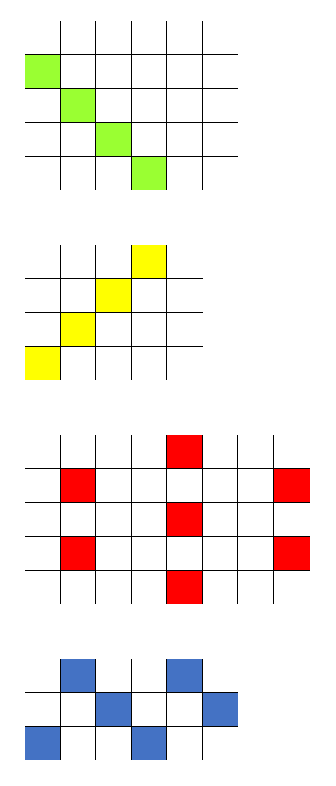
Under finn du fleire mønster, men her er det brukt frå firar-kart til niar-kart. Først er det laget mønster i eit sjuar-kart, så i eit femmar-kart, eit åttar-kart og eit seksar-kart. Kva tal er det som lagar dei ulike mønstera? Kan du forklare kvifor mønstera blir slik i desse karta?
No kan du utforske mønster sjølv. Du kan bruke dette rutearket når du eksperimenterer. Kva tal er det som lagar diagonalar i dei ulike karta? Er det nokon samanheng mellom kartstorleiken og tala som lagar diagonalar i dei ulike karta?
Kva tal er det som lagar vertikale linjer i dei ulike karta? Er det nokon samanhengar her?
Prøv å lage nokre av dei andre mønstera i andre kart. Kva mønster klarer du å lage, og i kva kart klarer du å lage dei?
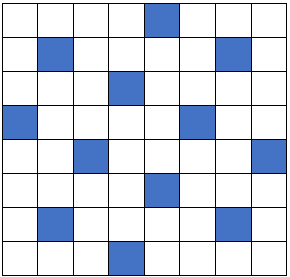
No er du kanskje klar for ei større utfordring? Du får ikkje sjå heile kartet, berre dei øvste radene. Prøv å finne ut kva kart som er brukt, og kva tal som lagar dette mønsteret. Det kan hende du treng rutepapir for å løyse oppgåva. Det finn du her.
No kjem den største utfordringa! Klarer du å finne ut kva kart og kva tal som lagar mønstera under? Her får du sjå berre delar av karta, og sidene på karta blir ikkje viste. NB! Det kan finnast meir enn éi løysing.
Løysing
Omar og Peter seier at dei har funne ut følgjande:
- Viss det blir eit mønster der kvar fjerde rute er fargelagd, vil mønsteret innehalde multiplarMultippel er produktet av eit gitt tal og eit heiltal. Talet 8 ein multippel av talet 2, men også av 4, sidan 8 er deleleg med både 2 og 4. av 4, og viss kvar sjette rute er fargelagd, vil mønsteret innehalde multiplar av 6, osb.
- I sjuar-kartet er kvar tredje rute fargelagt, altså multiplar av 3, så talet 3 lager mønsteret.
- I femmar-kartet er annakvar rute fargelagt, og alle er multiplar av 2. Derfor er det 2 som lagar mønsteret. Vi fann også ut at på eit oddetalskart (t.d. sjuar-kart eller niar-kart) vil 2 laga eit mønster som på eit sjakkbrett, medan viss det er eit partalskart (t.d. seksar-kart eller åttar-kart), vil 2 laga eit mønster med vertikale linjer.
- I åttar-kartet er kvar femte rute fargelagt (multiplar av 5). Derfor er det 5 som lagar mønsteret.
Bente og Pari har undersøkt når mønsteret blir diagonalar, og funne ut følgjande:
- I seksar-kartet blir det diagonalar når vi fargelegg med tala 5 og 7.
- I sjuar-kartet blir det diagonalar når vi fargelegg med tala 6 og 8. Derfor trur vi at blir det diagonalar når vi fargelegg tala som er éin meir eller éin mindre enn talet på ruter i kartet. Vi prøvde for niar-kartet etterpå, og då vart det diagonalar med tala 8 og 10.
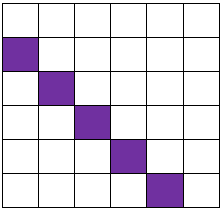
Kine og Lisa har undersøkt karta som ikkje har sidekantar, og dei har funne ut følgjande:
- I det første kartet er det ein diagonal som starter på den andre linja, og det er i alle fall 6 ruter i kartet. Det betyr at talet som lagar mønsteret, må vere éin større enn kartet. Vi trur derfor at kartet kan vere eit seksar-kart eller større, og at talet som lagar mønsteret, er éin meir enn kartstorleiken.
- Det andre mønsteret lagar ein diagonal som går andre vegen. Derfor trur vi at talet som lagar dette mønsteret, er éin mindre enn kartstorleiken. Då kan kartet vere eit femmar-kart, og talet som lagar mønsteret, kan vere 4.
- I det neste kartet blir mønsteret laga i kvar sjette rute. Derfor må talet som lagar mønsteret, vere 6. Viss vi skal klare å lage dette mønsteret med 6, må det vere eit 15-kart.
- I det siste mønsteret blir kvar tredje rute fargelagd. Det betyr at talet som lagar mønsteret, må vere 3. Mønsteret blir forskove éi rute mot høgre for kvar rad. Vi får til å teikne mønsteret i eit åttar-kart. Kartet kan også utvidast med 3, eller med multiplar av 3. Mønsteret kan derfor teiknast i 8-kart, 11-kart, 14-kart, 17-kart, 20-kart, 23-kart osb.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Arbeid med dette problemet kan auke forståinga til elevane av faktorar og multiplar. Det kan også vere eit spennande arbeid som gir betre forståing av multiplikasjon. Elevane kan lage hypotesar og prøve dei ut. Aktiviteten kan dessutan gi høve til å introdusere ideen om at ein bokstav kan stå for kva tal som helst.
Elevane kan også få auka forståing av mønster og design.
Mogleg tilnærming
Arbeid med dette problemet kan starte med at elevane fargelegg mønster ut frå gongetabellane i eit vanleg 100-kart. Det er viktig at mønstera ikkje alltid blir rette linjer, så elevane kan godt fargeleggje 3-gangen og 4-gangen før dei tek 2-gangen og 5-gangen. Spør kvifor 2-gangen og 5-gangen blir rette linjer. Bruk ordet faktor når det er formålstenleg.
Viss elevane allereie har gjort ein del av slikt arbeid, kan du snakke om kva som dannar rette linjer, og kvifor. Gi elevane deretter eit unummerert tiar-kart (10 x 10 ruter). Du finn det i menyen til venstre. Be ulike læringspar fargeleggje ulike gongetabellar i tiar-kartet. Be dei prøve å føresjå kva mønster det vil bli, før dei fargelegg. Elevane kan i staden krysse ut dei rutene som dannar mønsteret, for fargelegging kan ta for lang tid.
No kan de sjå på dei ulike karta. Elevane kan arbeide i par og dele idear, funn og refleksjonar.
Det finst to kopioriginalar med ulike kart og mønster. Desse kopioriginalane har fleire kart enn i oppgåva som ligg på nettet. På kopioriginal A ligg det eit kart til første del av oppgåva, og på kopioriginal B finst det utsnitt av kart der sidekantane manglar. Oppgåvene i B er meir krevjande enn oppgåvene i A, og dei kan ha fleire rette svar. Ruteark kan vere nødvendig når elevane skal arbeide med desse oppgåvene.
Mot slutten av undervisningsøkta kan elevane forklare korleis ulike mønster oppstår i ulike kart. Diskuter faktorane i talet som beskriv storleiken på kartet. Det bør de også gjere med tala som er éin meir og éin mindre. I dette sambandet kan du innføre ein bokstav som står for kva tal som helst. Elevane kan dessutan diskutere kva som skaper spennande mønster som fyller store delar av karta.
Gode rettleiingsspørsmål
- Hvilket mønster trur de at de vil få her?
- Kva tal gir vertikale linjer? Kvifor trur de det er sånn?
- Kva tal dannar diagonalar? Kvifor gjer dei det?
- Kva typar kart og tal trur de dannar sjakkrutemønster?
- Kva er det som dannar spennande mønster som fyller store delar av karta?
Mogleg utviding
Elevar som blir tidleg ferdige og har gode forklaringar på svara sine, kan lage liknande oppgåver til medelevane sine.
Elevane kan prøve å føresjå og arbeide i sjuar-kart og tolvar-kart. Dei kan også prøve å uttrykkje funna sine algebraisk.
Mulig støtte
La elevane bruke eit nummerert 100-kart og undersøkje mønster i det..
Ressursen er utviklet av NRICH