Skiftande areal, skiftande omkrins
Aktivitet
Her er ni figurar. Du kan skrive dei ut frå kopioriginalen i menyen.
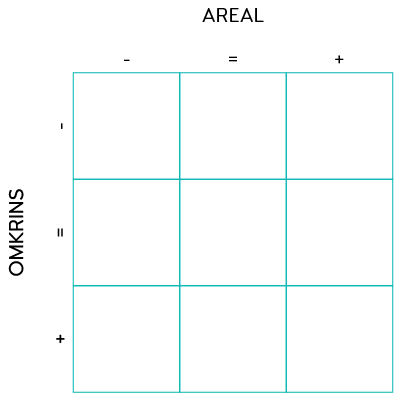
Utfordringa er å plassere figurane i rutenettet under.
Når du går frå venstre til høgre, aukar arealet av figuren.
Når du går frå toppen til botnen, aukar omkrinsen til figuren.
Alle figurane i den midtarste kolonnen har same areal.
Alle figurane i den midtarste rada har same omkrins.
Korleis kan du resonnere for å avgjere kvar du skal plassere kvar figur?
Her er dimensjonane til ni rektangel. Desse kan du skrive ut frå kopioriginalen i menyen til venstre.
| \(2\cdot8\) | \(4\cdot4\) | \(1\cdot15\) |
| \(5\cdot5\) | \(3\cdot8\) | \(2\cdot7\) |
| \(1\cdot16\) | \(3\cdot6\) | \(1\cdot9\) |
Kan du plassere desse rektangla i eit rutenett på same måten?
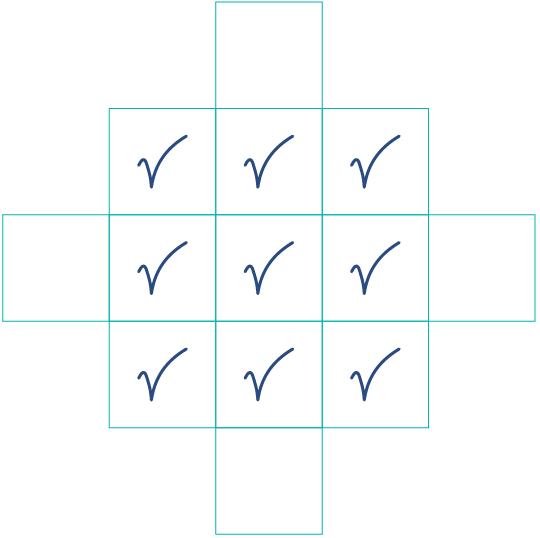
Når du har plassert dei ni korta, kan du sjå på rutenettet under.
Hakane representerer dei ni korta du alt har plassert.
Kan du lage kort med dimensjonar for rektangel som kan plasserast i dei fire tomme rutene, og som oppfyller dei same kriteria?
Det er ikkje mogleg å fylle alle rutene. Kan du forklare kvifor?
Kan du lage eit sett med kort som kan plasserast på same måten, dersom kortet i midten er eit rektangel med dimensjonar 1 · 5?
Starthjelp
Dersom du synest det er vanskeleg å forstå rutenettet, kan du ta ein titt på dette biletet.
Robotane er plasserte ut frå breidde og høgde, på same måten som korta skal plasserast etter areal og omkrins:
Når du går frå venstre til høgre, aukar breidda på roboten.
Når du går frå toppen til botnen, aukar høgda på roboten.
Alle robotane i den midtarste kolonnen har same breidda.
Alle robotane i den midtarste rada har same høgda.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Når elevane arbeider med denne oppgåva, kan dei få djupare forståing av areal og omkrins, og korleis desse storleikane endrar seg når forma på figuren blir endra. Aktiviteten tek for seg den misoppfatninga at når arealet aukar, må også omkrinsen auke.
Mogleg tilnærming
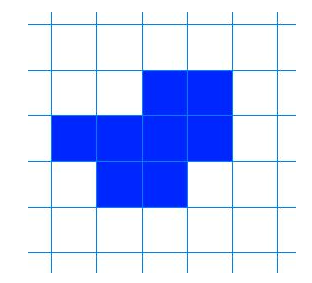
Vis fram ein enkel figur laga av kvadrat i eit rutenett, for eksempel denne:
«Bruk eit ruteark, og fargelegg kvadrat slik at de får ein annan figur enn min, men med same arealet.»
«Min figur har omkrins 14. Har nokon andre ein figur med omkrins 14?»
Samle inn eksempel og vis dei fram.
«Har nokon ein figur med omkrins mindre enn 14?»
Vis fram eksempla.
«Har nokon ein figur med omkrins større enn 14?»
Vis fram eksempla.
Dersom nokre av kategoriane ikkje har eksempel i klassen, kan du utfordre elevane til å lage høvelege figurar.
«Areal og omkrins er to av kjenneteikna/eigenskapane ved desse figurane. På dette biletet er robotane plassert etter kjenneteikna sine. Kan de finne ut korleis dei er plasserte?»
Trekk fram nøkkelideane:
Når du går frå venstre til høgre, aukar breidda på roboten.
Når du går frå toppen til botnen, aukar høgda på roboten.
Alle robotane i den midtarste kolonnen har same breidda.
Alle robotane i den midtarste rada har same høgda.
Vis fram dette biletet av robotane for å summere opp det elevane (vonleg) har lagt merke til. Vis også rutenettet som dei skal bruke i resten av aktiviteten.
«Vi kan plassere figurane i eit rutenett på 3 · 3 på same måten, ved å sortere dei etter areal og omkrins i staden for etter høgde og breidde.»
Gi kvart elevpar korta (kopioriginal Ni figurer) til den første utfordringa, vis rutenettet på tavla, og forsikre deg om at elevane veit kva dei skal gjere.
Når para blir ferdige, kan dei få det andre settet med kort (kopioriginal Ni rektangler) og arbeide på same måten. Dei som blir fort ferdige, kan arbeide med eit utvida rutenett, som dette:
Mot slutten av timen samlar du klassen og deler effektive måtar elevane fann for å samanlikne areal og omkrins.
Når de ser på tilbakemeldingar frå den første utfordringa, kan du spørje elevane kva dei la merke til om figurane i den øvste rada i rutenettet.
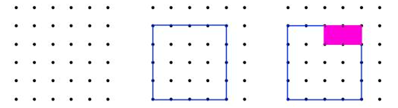
For å forklare kvifor omkrinsen er 16 for alle figurar som blir teikna ved å kutte hjørna på eit kvadrat som er 4 · 4, kan desse bileta vere til hjelp:
«Kor mykje av omkrinsen mistar ein når ein kuttar av det rosa rektangelet? Kor stor omkrins får ein?»
Figurar på den andre og tredje rada kan samanliknast på same måten.
Med den andre utfordringa vil vi få elevane til å innsjå dette:
«Rektangel som er nærare kvadrat, har mindre omkrins enn lange, tynne rektangel med same arealet.»
Eit spørsmål som kan trekkjast ut frå dette, er:
«Dersom to rektangel har det same arealet, korleis kan eg finne ut kven av dei som har størst omkrins?»
Diskuter til slutt det moglege innhaldet i dei fire tomme rutene i det utvida rutenettet, og fokuser særleg på kvifor det er umogleg å fylle somme av dei.
Mogleg utviding
Elevane kan til slutt lage sitt eige sett med kort, der eit rektangel med dimensjonar 1 · 5 er kortet i midten. Dette tvingar dei til å vurdere rektangel med sidelengder som ikkje er heiltal.
Ressursen er utviklet av NRICH