Skiftande overflate, skiftande volum
Aktivitet
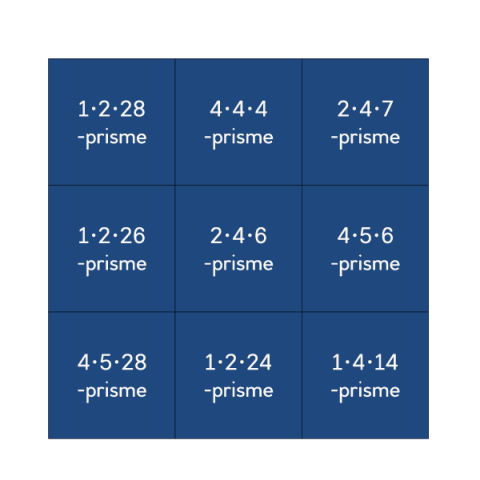
Nedanfor ser du måla på ni forskjellige prisme. Du kan også laste ned ein kopioriginal som viser den same tabellen.
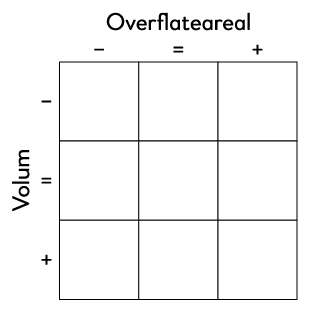
Utfordringa er å organisere prisma i ein slik \(3\cdot3\)-tabell:
- Når du går frå venstre til høgre i tabellen, skal overflatearealet av prismet auke.
- Når du går frå toppen og nedover i tabellen, skal volumet av prismet auke.
- Alle prisme i den midtarste kolonnen skal ha same overflateareal.
- Alle prisme i den midtarste rada skal ha same volum.
Korleis kan du resonnere deg fram til rutene der kvart av dei ni prisma skal plasserast?
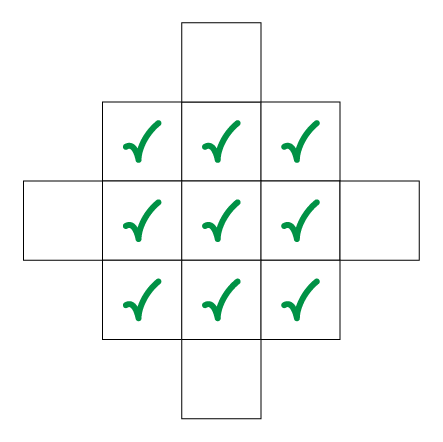
Når du har plassert dei ni korta, kan du sjå på dette utvida rutenettet:
Dei grøne hakane representerer dei ni korta du alt har plassert. Kan du lage kort med mål til ulike prisme som kan plasserast i dei fire tomme rutene, slik at dei oppfyller dei same krava?
Kan du lage dine eigne kort med eit anna prisme i midten?
Starthjelp
- Dersom du veit at to rektangel har same areal, korleis kan du vite kva for eit som har størst omkrins?
- Dersom du veit at to prisme har same volum, korleis kan du vite kva for eit som har størst overflate?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva kan gi elevane djupare forståing av forholdet mellom volum og overflate, og korleis dei endrar seg når måla på eit prisme blir endra.
Mogleg tilnærming
Bruk litt tid på å forklare oppbygginga av rutenettet, og skriv gjerne inn nokre eksempelprisme som ikkje er med i oppgåva.
Når elevane kjenner til oppbygginga av rutenettet, kan du dele ut kopioriginalen med korta og tabellane. La elevane arbeide saman i par med å fylle ut det første rutenettet.
Elevane kan også bruke multilink-kubar eller teikne kvart prisme på isometrisk papir. Det kan vere til god hjelp for dei i arbeidet med oppgåva.
Dei som blir fort ferdige, kan gå vidare med det utvida rutenettet.
Mot slutten av arbeidsøkta kan du samle elevane slik at dei kan dele effektive strategiar dei har brukt for å løyse oppgåva.
Still spørsmål som dette: «Dersom eg veit at to prisme har likt volum, korleis kan eg bestemme, berre ved å sjå på måla, kva for eit av prisma som har størst overflate?»
Få fram tankar hos elevane om eigenskapane til lange og tynne prisme, samanlikna med prisme som er tilnærma kubiske. Dette er den tredimensjonale varianten av at eit kort og nesten kvadratisk rektangel har mindre omkrins enn eit langt og tynt, sjølv om dei har same areal.
Avslutt med å diskutere moglege mål på prisma som kan plasserast i dei fire tomme rutene i det utvida rutenettet.
Mogleg utviding
Elevane kan lage sine eigne sett med ni prismekort og plassere dei på same måten som i oppgåva. Dersom dei berre skal bruke heiltal, er det nokså utfordrande å lage prisme med lik overflate.
Ressursen er utviklet av NRICH